[Gianluca Gorni's home page]

Lecture Notes (in Italian)

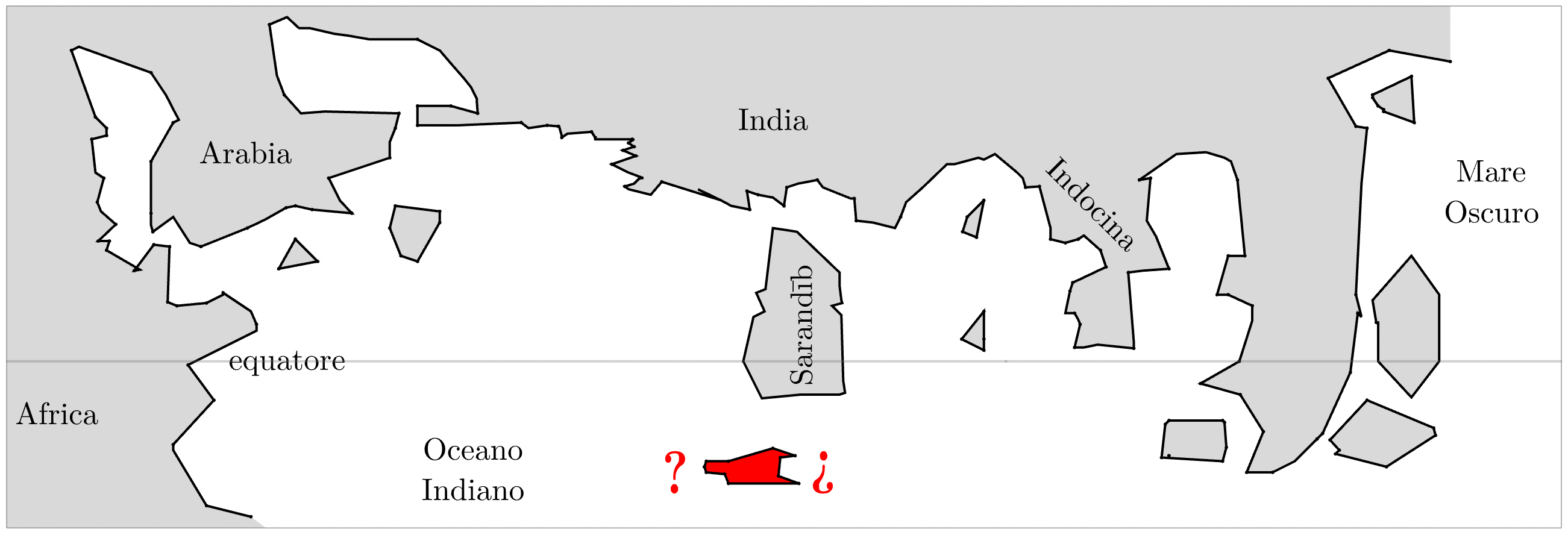
Video recording of a conference of mine (in Italian) on ancient geography, entitled "The island which is not there".

• YouTube video recording of a lecture: Spatial interaction and functional response in Lotka-Volterra prey-predator systems. By Elena Bozzetto, Gianluca Gorni. A graduation work in Mathematics at Udine University, Italy. Evento em homenagem aos 75 anos do Profº Ângelo Barone Netto. IME-USP, São Paulo, Brasil, 2011-08-01. An interdisciplinary topic: biology/ecology, differential equations, probability, special functions, computer stochastic simulation.
  
• Registrazione YouTube di una lezione di Istituzioni di Analisi Superiore del 2021-04-16 all'Università di Udine, in cui si usano animazioni per far capire l'idea sottostante al Teorema delle infinite estrazioni di sottosuccessioni col metodo diagonale. Enunciato: se abbiamo una matrice reale a due indici $A_n(k)$, con $n,k\in\N$, tale che l'insieme $\{A_n(k): n\in\N\}$ sia limitato per ogni~$k\in\N$, allora esiste una $\varphi\colon\N\to\N$ strettamente crescente tale che la successione $n\mapsto x_{\varphi(n)}(k)$ converge per ogni~$k$ fissato. Il teorema schiude le applicazioni della compattezza a spazi a dimensione infinita.
  
• YouTube playlist of three recorded lectures (in Italian) on a visual introduction to the functions of two variables.
  
  Mathematica file. You can view it with the free Wolfram Player). Mathematica notebook (152MB)


• YouTube playlist of two recorded lectures (in Italian) on a visual introduction to the concept of derivative of a function, based on the idea of zooming into the graph of the function.
  
  Mathematica file. You can view it with the free Wolfram Player). The two YouTube lectures separately: Lecture on YouTube, part 1, Lecture on YouTube, part 2.


• YouTube playlist of three recorded lectures (in Italian) as an introduction to the concept of limit, based on animated decimal numbers and a soccer-like game.
  
  Mathematica file. You can view it with the free Wolfram Player. The two YouTube lectures separately: Lecture on YouTube, part 1, Lecture on YouTube, part 2, Lecture on YouTube, part 3. page.


• YouTube video of a recorded lecture (in Italian) about the mean value theorems of Rolle, Lagrange and Cauchy.
  
• YouTube playlist of two recorded lectures (in Italian) as an introduction to the integral of a function.
  
  PDF file. Also: printable text summary. The two YouTube lectures separately: Lecture on YouTube, part 1, Lecture on YouTube, part 2.


• YouTube playlist of twelve recorded lectures (in Italian) on an introduction to LaTeX, a system for writing mathematics by computer.
  


• Lecture notes on Hilbert spaces and compact operators (2.7MB).
• Using your fingers to count in base 16 (42K).
• The Greek alphabet, for use in mathematics and computer science (69K).
• Cardano's solution to the third degree equation (140K).
• The induction principle (100K)
• Set theory (229K).
• Set-theoretic relations (120K).
• Peano's axioms (153K).
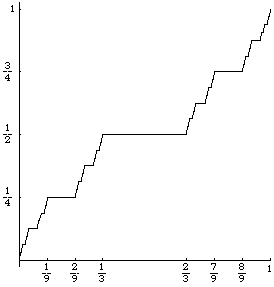
• Infinite cardinalities (116K).
• The square root of 2 (442K).
• Uniform continuity in dimension 1 (164K).
• Iterating functions of one variable (118K).
• Some "pathological" functions of one variable (188K).
• Limit points of a sequence of real numbers (104K).
• The sequence of the powers of a complex number (138K).
• Some different ways of making R^2 a normed space (89K).
• Cantor's set and Peano's curve (237K). See also the companion Mathematica notebook and Peano's curve QuickTime Movie (700K).
• Van der Waerden's nowhere differentiable function (256K); see also the companion Mathematica notebook.
• Some aspects of the complex exponential function explained through pictures (248K).
• An elementary proof of the fundamental theorem of Algebra (95K).
• A pictorial introduction to functions of two variables (2.9 MB). Mathematica notebook (152MB)
• Double integrals through pictures (16MB). You can view it with the free Wolfram CDF Player.
• Some examples of integration in two variables (7MB).
• A videogame to illustrate the definition of limit (32K). You can view it with the free Wolfram CDF Player.
• A summary of indeterminate limits, with final quiz (32K). You can view it with the free Wolfram CDF Player.
• A tutorial on the mean value theorems by Rolle, Lagrange and Cauchy. You can view it with the free Wolfram CDF Player). Lecture on YouTube
• Animations to visualize real-valued functions on the unit circle, to set the stage for Fourier analysis. (You can view the cdf with the free Wolfram CDF Player)
• Animations to visualize the complex powers on the unit circle
• Pictures to illustrate trigonometric Fourier series: pdf version (633K) and cdf version with animations (37M).
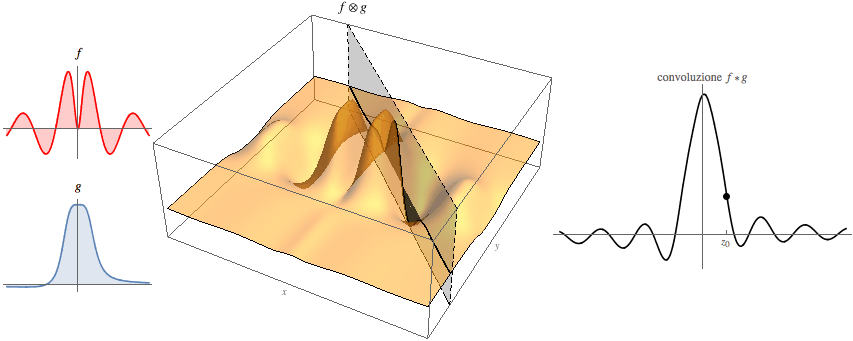
• The convolutions of functions explained with pictures.
• Fourier approximants visualized as composition of uniform circular motions.
• The Hahn-Banach theorem illustrated (290K) (You can view the cdf with the free Wolfram CDF Player)
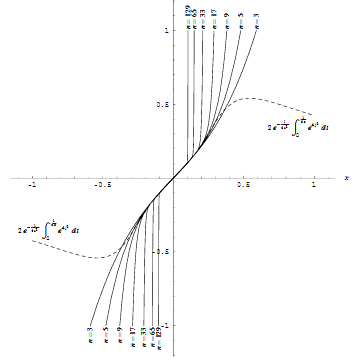
• Semiintegrable and measurable functions (160K).
• Illustrations on Taylor polynomials in pdf format and in cdf format.
• Construction of Lebesgue measure in Euclidean space.
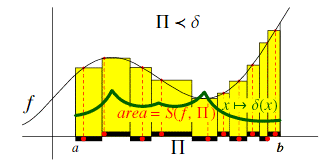
• Vitali-Lebesgue's theorem on the relation between Riemann and Lebesgue integration.
• Lusin's theorem on the approximations of a measurable function with continuous functions.
• The orthogonal projection onto the closed subspace generated by an orthonormal system in a Hilbert space.