Progetto di laboratorio AA 2009/2010

La teoria dei sei gradi di separazione è un'ipotesi secondo cui qualunque persona è collegata a qualunque altra persona attraverso una catena di conoscenze di lunghezza media pari a 6 (cioè con 5 intermediari). Nel 1967 il sociologo americano Stanley Milgram verificò questa teoria su un gruppo casuale di americani del Midwest e coniò l'espressione piccolo mondo (small world) per descrivere la brevità della catena di separazione rispetto al numero di persone della rete sociale.

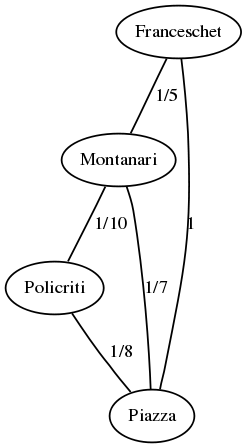
Il progetto ha come obiettivo la stima del grado di separazione accademico sull'intera comunità internazionale di ricercatori in Informatica. Un grafo di collaborazione è un grafo indiretto in cui i nodi sono ricercatori e gli archi rappresentano collaborazioni accademiche: esiste un arco tra gli autori A e B se essi hanno collaborato nella scrittura di almeno un articolo e ne sono co-autori. In un grafo di collaborazione pesato gli archi hanno associato un peso pari alla frazione 1/n, dove n è un intero positivo che corrisponde al numero di articoli che gli autori hanno scritto assieme. Dunque il peso è un reale in (0,1] che rappresenta la prossimità accademica tra due autori: essi sono tanto più vicini quanto è maggiore il numero di lavori che hanno prodotto in collaborazione. Un semplice esempio di grafo di collaborazione pesato è rappresentato in figura, la cui rappresentazione GraphViz è contenuta nel file sample.dot:

GraphML è un formato testuale di grafi basato sul linguaggio XML. In questa rappresentazione i nodi del grafo sono rappresentati dagli elementi XML chiamati node: l'attributo id dell'elemento è un identificatore numerico univoco dell'autore, l'elemento data contiene il nome del ricercatore. Gli archi del grafo sono rappresentati dagli elementi XML edge: gli attributi source e target contengono gli identificatori degli autori che formano l'arco, l'elemento data contiene il numero di articoli scritti in collaborazione dagli autori che formano l'arco (e non il suo reciproco). La rappresentazione GraphML del grafo in figura è contenuta nel documento sample.xml.

Un esempio più esteso di grafo di collaborazione è rappresentato nella figura che segue (formato GraphML; formato GraphViz):

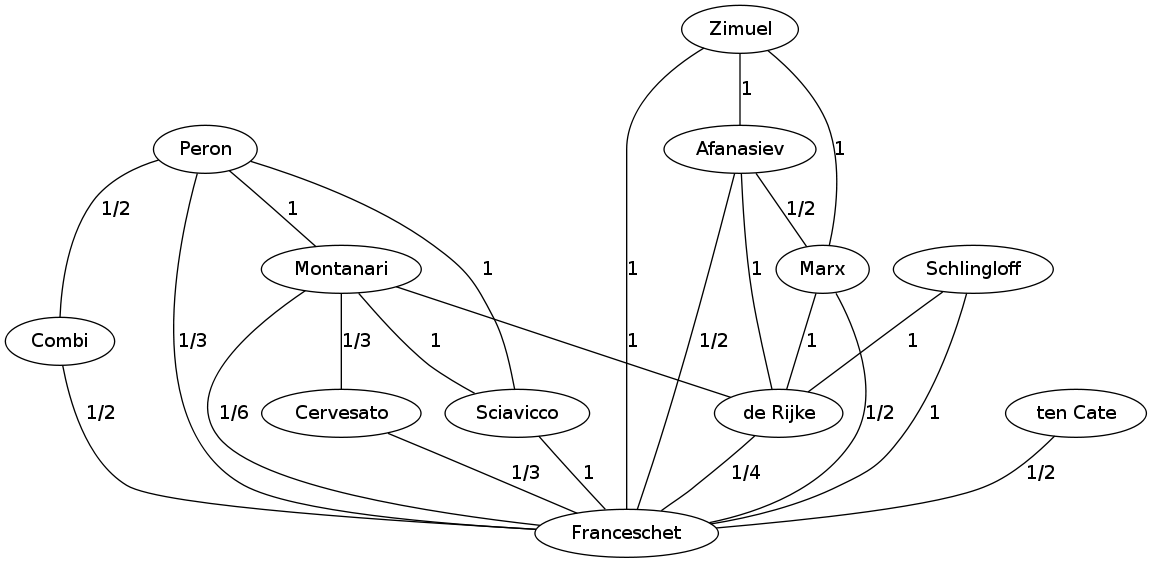
Dato un grafo e un relativo cammino P, definiamo lunghezza di P il numero di archi contenuti in P, e definiamo peso di P la sommatoria dei pesi degli archi di P. La distanza tra due nodi A e B è la lunghezza di un cammino di lunghezza minima che connette A e B. La distanza pesata tra due nodi A e B è il peso di un cammino di peso minimo che connette A e B. Il grado di un nodo è il numero di nodi adiacenti a quel nodo (ovvero il numero di archi che contengono quel nodo).

Il primo obiettivo del progetto è scrivere in Java una classe che implementi in modo efficiente i seguenti metodi:

un metodo che legge un grafo di collaborazione da un documento in formato GraphML e carica in memoria il grafo usando una rappresentazione a liste di adiacenza (ricordarsi di assegnare come peso degli archi il reciproco del numero di articoli co-prodotti che si legge nel documento XML);
un metodo che salva il grafo di collaborazione caricato in formato GraphViz con nodi etichettati con il cognome del ricercatore e archi etichettati con il loro peso;
un metodo che, dati i nomi di due ricercatori, restituisce un cammino di lunghezza minima tra i due ricercatori nel grafo di collaborazione caricato, nonché la lunghezza e il peso del cammino trovato;
un metodo che, dati i nomi di due ricercatori, restituisce un cammino di peso minimo tra i due ricercatori nel grafo di collaborazione caricato, nonché la lunghezza e il peso del cammino trovato;
un metodo che genera un campione casuale significativo di coppie di nodi del grafo di collaborazione caricato e per ogni coppia di nodi calcola un cammino di lunghezza minima che connette i due nodi, memorizzando la sua lunghezza e il suo peso. Il metodo deve inoltre calcolare la media tra le lunghezze e i pesi misurati sull'insieme delle coppie generate.
un metodo che genera un campione casuale significativo di coppie di nodi del grafo di collaborazione caricato e per ogni coppia di nodi calcola un cammino di peso minimo che connette i due nodi, memorizzando la sua lunghezza e il suo peso. Il metodo deve inoltre calcolare la media tra le lunghezze e i pesi misurati sull'insieme delle coppie generate.
un metodo che genera la sequenza dei gradi dei nodi del grafo di collaborazione caricato.

La classe Java scritta deve interfacciarsi con l'utente mediante una console da linea di comando che permette all'utente di richiedere una qualsiasi delle operazioni implementate, richiedendo all'utente opportuni dati quando necessario.

Il secondo obiettivo del progetto è applicare il codice scritto al grafo di collaborazione dell'intera comunità mondiale di ricercatori di Informatica, la cui versione GraphML è contenuta nel seguente archivio: cg.xml.zip. Si noti che il file decompresso ha dimensione 220,5 MB e il grafo di collaborazione contiene 747.013 nodi e 2.533.879 archi, dunque in questa fase verrà testata l'efficienza dei metodi scritti nella prima parte del progetto. In particolare, calcolare una stima del grado di separazione semplice e pesato e generare, salvandola, la sequenza dei gradi dei nodi. Si noti che è possibile aumentare lo spazio heap per la macchina virtuale Java con l'opzione -Xmx seguita dallo spazio da allocare. Per esempio, per allocare 2000 MB di spazio, usare il comando java seguito dall'opzione -Xmx2000m, seguito dal nome della classe da invocare.

Il terzo e ultimo obiettivo del progetto consiste nell'usare lo strumento statistico R per studiare la distribuzione dei gradi dei nodi del grafo di collaborazione dell'intera comunità mondiale di ricercatori di Informatica, generata al passo precedente. Usare strumenti di statistica descrittiva e confronti con opportuni modelli di distribuzioni teoriche, così come visto durante la parte del laboratorio su R.