L'obiettivo è studiare una rete sociale di delfini (Tursiops truncatus) appartenenti ad una comunità che vive nel fiordo di Doubtful Sound in Nuova Zelanda. Le condizioni inusuali di questo fiordo, con acqua relativamente fredda e con uno strato di acqua dolce in superficie, hanno limitato le uscite di esemplari e l'arrivo di nuovi delfini nel gruppo, facilitando una intensa relazione sociale tra i delfini della comunità.
La rete è un grafo indiretto che contiene 62 nodi delfini e 159 connessioni non direzionali tra coppie di delfini. Due delfini sono associati da un arco se, nel periodo di osservazione durato dal 1994 al 2001, essi sono stati avvistati assieme più frequentemente di quanto il caso avrebbe voluto. E' noto il sesso di quasi tutti gli esemplari.
Avviare R da un terminale con l'omonimo comando e, se non già fatto, installare il pacchetto igraph per l'analisi delle reti col comando e il pacchetto RGL per la visualizzazione 3D:
install.packages("igraph")
install.packages("rgl")
quindi caricare i pacchetti installati con il comando:
library(igraph) library(rgl)
Importare in R la rete dolphin.gml, in formato GML, usando il comando:
g = read.graph(file="dolphin.gml", format="gml")
Notate che i nodi hanno tre attributi: id (un identificatore numerico), label (il nome del delfino), e sex (il sesso, M per maschio, F per femmina, U per sconosciuto). Visualizzare il numero di nodi e il numero di archi del grafo. Calcolare la densità del grafo (numero di archi del grafo fratto numero massimo di archi del grafo). Dire se il grafo è sparso o denso. Contare il numero di esemplari maschi e femmine e la relativa percentuale.
n = vcount(g) m = ecount(g) 2* m / (n * (n-1)) graph.density(g) sex = V(g)$sex male = sex == "M" female = sex == "F" shemale = sex == "U" n.male = sum(male) n.female = sum(female) round(100 * (n.male / n)) round(100 * (n.female / n))
Visualizzare la rete con il metodo di Fruchterman e Reingold (layout.fruchterman.reingold) usando come etichette dei nodi il nome del delfino, oppure il suo identificatore numerico, oppure nessuna etichetta. Visualizzare i nodi femmina in rosa e i nodi maschi in blu. Visualizzare il sottografo delle femmine e quello dei maschi. Provare altre visualizzazioni: casuale (layout.random), circolare (layout.circle) e sferica (layout.sphere).
coords = layout.fruchterman.reingold(g) plot(g, layout=coords, vertex.label=V(g)$label, vertex.shape="none") plot(g, layout=coords, vertex.label=V(g)$id, vertex.size=8) plot(g, layout=coords, vertex.label=NA, vertex.size=5) V(g)[male]$color = "blue" V(g)[female]$color = "pink" V(g)[shemale]$color = "green" plot(g, layout=coords, vertex.label=NA, vertex.size=5) g.male = induced.subgraph(g, V(g)[male]) coords.male = layout.fruchterman.reingold(g.male) plot(g.male, layout=coords.male, vertex.label=NA, vertex.size=5) g.female = induced.subgraph(g, V(g)[female]) coords.female = layout.fruchterman.reingold(g.female) plot(g.female, layout=coords.female, vertex.label=NA, vertex.size=5) plot(g, layout=layout.random(g), vertex.label=NA, vertex.size=5) plot(g, layout=layout.circle(g), vertex.label=NA, vertex.size=5) plot(g, layout=layout.sphere(g), vertex.label=NA, vertex.size=5)
Visualizzare la rete in 3D con il metodo di Fruchterman e Reingold.
coords3D = layout.fruchterman.reingold(g, dim=3) rglplot(g, layout=coords3D, vertex.size=5, vertex.label.dist=0.2)
Trovare i gradi dei nodi. Calcolare le seguenti statistiche descrittive della distribuzione dei gradi: minimo, massimo, media, mediana, primo e terzo quartile. Generare un istogramma dei gradi dei nodi. Etichettare il vettore dei gradi con i nomi dei delfini e visualizzarlo in ordine decrescente rispetto al grado. Calcolare il grado medio degli esemplari femmina e maschio.
d = degree(g) summary(d) par(family = "serif") hist(d, xlab="Grado", ylab="Frequenza", main="Istogramma dei gradi dei nodi", breaks=0:max(d)) names(d) = V(g)$label sort(d, decreasing=TRUE) mean(d[male]) mean(d[female])
Verificare il paradosso degli amici sul grafo dei delfini. In dettaglio:
$\displaystyle{\mu_1 = \frac{\sum_i k_i}{n}$e la media dei gradi dei vicini dei nodi:
$\displaystyle{\mu_2 = \frac{\sum_{i,j} a_{i,j} k_j}{\sum_i k_i}$
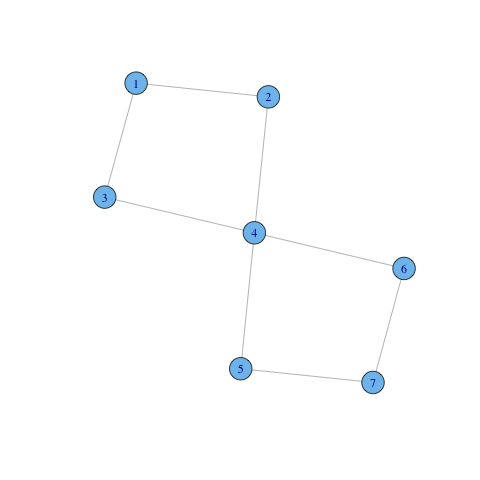
Dato un intero positivo k, una componente k-connessa di un grafo è un insieme massimale di nodi tali che ogni coppia di nodi è collegata da almeno k cammini indipendenti, cioè che non condividono nodi a parte il primo e l'ultimo. Vale che una componente k-connessa rimane connessa (nel senso ordinario del termine) se si rimuovo meno di k nodi, dunque la connettività è una misura della robustezza della rete. Una componente 1-connessa può contenere una o più componenti 2-connesse (possibilmente sovrapposte), le quali possono contenere una o più componente 3-connessa e così via. Si forma così una gerarchia (un albero) di componenti k-connesse.
In questo esempio il grafo è connesso e contiene due componenti biconnesse (k=2) composte dai nodi 1,2,3,4 e 4,5,6,7. Si noti che le componenti biconnesse non sono disgiunte.

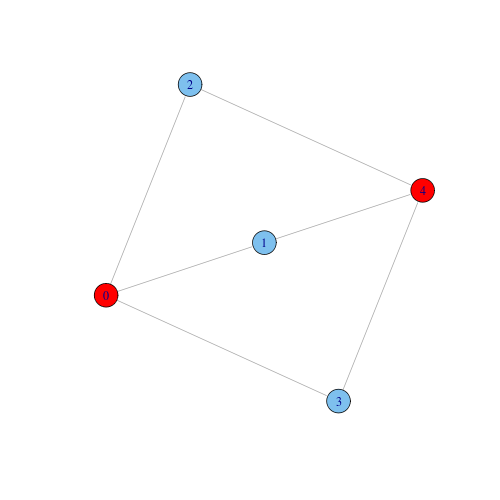
In questo esempio il grafo è biconnesso e contiene una componente triconnessa (k=3) composta dai nodi rossi 0 e 4. Si noti che la componente triconnessa non è contigua (il sottografo indotto non è connesso).
Trovare le k componenti e visualizzare la gerarchia. Colorare le componenti con connettività massima usando colori diversi.
blocks = cohesive.blocks(g) blocks b = blocks(blocks) b1 = b[[5]] b2 = b[[6]] V(g)$color = "white" V(g)[b1]$color = "blue" V(g)[b2]$color = "red" plot(g, layout=coords, vertex.label=NA, vertex.size=5)
Una cricca è un insieme di nodi del grafo tale che tutte le coppie di nodi sono connesse da un arco. Trovare le cricche più grandi e colorarle con colori differenti.
clique.number(g) clique = largest.cliques(g) V(g)$color = "white" for (i in 1:length(clique)) V(g)[clique[[i]]]$color = i plot(g, layout = coords, vertex.color = V(g)$color, vertex.label=NA, vertex.size=5)
Un insieme indipendente (o stabile) è un insieme di nodi del grafo in cui nessuna coppia di nodi è collegata da un arco. Trovare gli insiemi stabili più grandi e colorarne uno a piacere.
independence.number(g) stable = largest.independent.vertex.sets(g) s = stable[[1]] V(g)$color = "white" V(g)[s]$color = "red" plot(g, layout=coords, vertex.label=NA, vertex.size=5)
Il grafo complementare di un grafo si ottiene prendendo lo stesso insieme di nodi e il complementare dell'insieme degli archi (rispetto al prodotto cartesiano dei nodi). Notate che le cricche corrispondono agli insiemi indipendenti del grafo complementare e gli insiemi indipendenti corrispondono alle cricche del grafo complementare. Trovare il complementare del grafo e visualizzarlo. Verificare che la dimensione della massima cricca corrisponde alla dimensione del massimo insieme stabile nel complementare e che la dimensione del massimo insieme stabile corrisponde alla dimensione della massima cricca nel complementare.
gc = graph.complementer(g) V(gc)$color = "white" plot(gc, layout=layout.fruchterman.reingold(gc), vertex.label=NA, vertex.size=5) clique.number(g) independence.number(gc) independence.number(g) clique.number(gc)
Calcoliamo un albero di supporto (di costo minimo) e visualizzarlo nel grafo originale e separatamente come albero:
E(g)$id = 1:ecount(g) mst = minimum.spanning.tree(g, algorithm = "unweighted") E(g)$color = "grey" E(g)[E(mst)$id]$color = "red" plot(g, layout=coords, vertex.size=5, vertex.label=NA) E(g)$color = NA E(g)[E(mst)$id]$color = "red" plot(g, layout=coords, vertex.size=5, vertex.label=NA) plot(mst, layout=layout.reingold.tilford(mst), vertex.size=5, vertex.label=NA)
Trovare il grado di separazione (lunghezza media del cammino minimo tra due nodi) del grafo. Produrre un istogramma con le distanze tra i nodi del grafo. Trovare il diametro del grafo (lunghezza del più lungo cammino minimo). Visualizzare il grafo con i nodi e gli archi del diametro colorati in rosso. Trovare tutti i cammini minimi tra i due delfini al bordo del diametro.
average.path.length(g) p = path.length.hist(g) path = p$res names(path) = 1:length(path) barplot(path / sum(path), xlab="Distanza", ylab="Frequenza relativa") diameter(g) d = get.diameter(g) V(g)[d]$label E(g)$color = "grey" E(g)$width = 1 E(g, path=d)$color = "red" E(g, path=d)$width = 2 V(g)$color = "white" V(g)[d]$color = "red" plot(g, layout=coords, vertex.label = NA, vertex.size=5) x = d[1] y = d[length(d)] get.all.shortest.paths(g, from=x, to=y)
Immaginare che i delfini siamo fisicamente disposti in mare come nella visualizzazione ottenuta con le coordinate calcolate con il metodo di Fruchterman e Reingold. Usando l'algoritmo di approssimazione che usa l'albero di supporto di costo minimo, trovare un tour dei delfini, visualizzarlo, e calcolarne il relativo costo.
d = dist(coords) full = graph.full(vcount(g), directed=FALSE) E(full)$weight = as.vector(d) mst = minimum.spanning.tree(full, weights = E(full)$weight) dfs = graph.dfs(mst, root=1) tour = c(dfs$order, 1) cost = sum(E(full, path=tour)$weight) E(full)$color = NA E(full, path=tour)$color = "red" plot(full, layout=coords, vertex.label=NA, vertex.size=5)