The World Wide Web is modelled as a directed network in which nodes represent Web pages and edges are the hyperlinks between pages. More precisely, there exists an edge from page $p$ to page $q$ if page $p$ contains at least one hyperlink pointing to page $q$. Usually, the actual number of hyperlinks from $p$ page $q$ is not important and hence the network modelling the Web is unweighted. Moreover, page self-links are ignored.
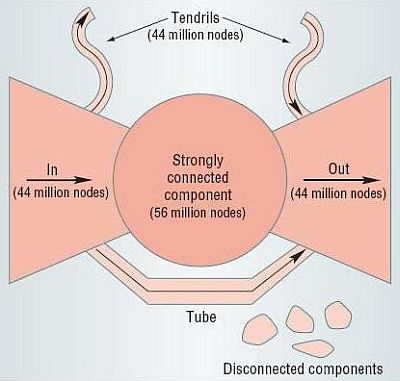
The Web network has a bow-tie fragmented structure. This structure predicts the existence of four main continents of roughly the same size:

This structure significantly limits the Web's navigability, that is, how far we can get taking off from a given node. Starting from any page, we can reach only about one quarter of all documents. The rest are invisible to us, unreachable by surfing. Since the Web is explored by robots which navigate from page to page following the page hyperlinks, this heavily influences our knowledge of the Web.
The most popular method to rank webpages according to their importance is Google PageRank, a variant of the eigenvector centrality measure. We briefly recall how the PageRank method works. The excellent book Google's PageRank and Beyond of Amy N. Langville and Carl D. Meyer elegantly describes the science of search engine rankings in a rigorous yet playful style.
Before giving the mathematical formulation of the problem solved by the PageRank method, we provide an intuitive interpretation of PageRank in terms of random walks on graphs. The Web is viewed as a directed graph of pages connected by hyperlinks. A random surfer starts from an arbitrary page and simply keeps clicking on successive links at random, bouncing from page to page. The PageRank value of a page corresponds to the relative frequency the random surfer visits that page, assuming that the surfer goes on infinitely. The higher is the number of times the random surfer visits a page, the higher is the importance, measured in terms of PageRank, of the page.
In mathematical terms, the method can be described as follows. Let us denote by $q_i$ the outgoing degree of page $i$ and let $H = (h_{i,j})$ be a square transition matrix such that $h_{i,j} = 1 / q_i$ if there exists a link from page $i$ to page $j$ and $h_{i,j} = 0$ otherwise. The value $h_{i,j}$ can be interpreted as the probability that the random surfer moves from page $i$ to page $j$ by clicking on one of the hyperlinks of page $i$. The PageRank $\pi_j$ of page $j$ is recursively defined as:
$\displaystyle{\pi_j = \sum_i \pi_i h_{i,j}}$
or, in matrix notation:
$\displaystyle{\pi = \pi H}$
Hence, the PageRank of page $j$ is the sum of the PageRank scores of pages $i$ linking to $j$, weighted by the probability of going from $i$ to $j$. In short, the PageRank thesis reads as follows:
A Web page is important if it is pointed to by other important pages.
Notice there are three distinct factors that determine the PageRank of a page:
The first factor is not surprising: the more links a page receives, the more important it is perceived. Reasonably, the link value depreciates proportionally to the number of links given out by a page: endorsements coming from parsimonious pages are worthier than those emanated by spendthrift ones. Finally, not all pages are created equal: links from important pages are more valuable than those from obscure ones.
Unfortunately, the described ideal model has two problems that prevent the solution of the system. The first one is due to the presence of dangling nodes, that are pages with no forward links. These pages capture the random surfer indefinitely. Notice that a dangling node corresponds to a row in $H$ with all entries equal to 0. To tackle the problem, such rows are replaced by a bookmark vector $b$ such that $b_i > 0$ for all $i$ and $\sum_i b_i = 1$. This means that the random surfer escapes from the dangling page by jumping to a completely unrelated page according to the bookmark probability distribution. Let $S$ be the resulting matrix.
The second problem with the ideal model is that the surfer can get trapped by a closed cycle in the Web graph, for instance, two pages A and B such that A links only to B and B links only to A. The solution proposed by Brin and Page is to replace matrix $S$ by Google matrix:
$\displaystyle{G = \alpha S + (1-\alpha) T}$
where $T$ is the teleportation matrix with identical rows each equal to the bookmark vector $b$, and $\alpha$ is a free balancing parameter of the algorithm. The interpretation is that, with probability $\alpha$ the random surfer moves forward by following links, and, with the complementary probability $1 - \alpha$ the surfer gets bored of following links and it is teleported to a random page chosen in accordance with the bookmark distribution. The inventors of PageRank propose to set $\alpha = 0.85$, meaning that after about five link clicks the random surfer chooses from bookmarks. The PageRank vector is then defined as the solution of equation:
$\displaystyle{\pi = \pi G}$
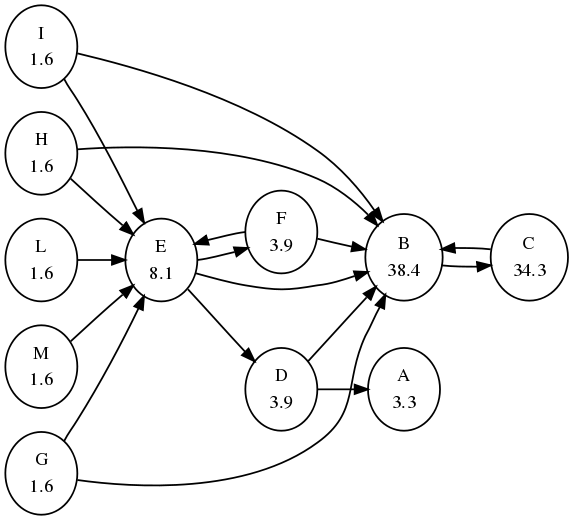
Figure above shows a PageRank instance with solution. Each node is labelled with its PageRank score; scores have been normalized to sum to 100 and are approximated to the first decimal point. We assumed $\alpha = 0.85$ and each bookmark probability equal to $1/n$, where $n = 11$ is the number of nodes. Node A is a dangling node, and nodes B and C form a dangling cycle. Notice the dynamics of the method: node C receives just one link but from the most important page B, hence its importance is higher than that of E, which receives much more links (5) but from anonymous pages. Pages G, H, I, L, and M do not receive endorsements; their scores correspond to the minimum amount of status assigned to each page.
Does the PageRank equation has a solution? In the solution unique? Can we efficiently compute the solution? The success of the PageRank method rests on the answers to these queries. Luckily, all these questions have nice answers.
Given a square matrix $A = (a_{i,j})$ of size $n$, the graph of $A$ is a directed graph with $n$ nodes $\{1,2, \ldots, n\}$ such that there is an edge from $i$ to $j$ if and only if $a_{i,j} \neq 0$. Matrix $A$ is irreducible if, for each pair of nodes $(i,j)$ in the graph of $A$ there is a path from $i$ to $j$; it is primitive if there exists $k > 0$ such that, for each pair of nodes $(i,j)$ in the graph of $A$ there is a path of length $k$ from $i$ to $j$.
Clearly, a primitive matrix is also irreducible. A fundamental result of algebra is the Perron-Frobenius theorem. It states that, if $A$ is an irreducible nonnegative square matrix, then there exists a unique vector $x$, called the Perron vector, such that $x A = rx$, $x > 0$, and $\sum_i x_i = 1$, where $r$ is the maximum eigenvalue of $A$ in absolute value, which is called the spectral radius $\rho(A)$ of $A$.
Matrices $S$ and $G$ used in PageRank formulation are both stochastic matrices with spectral radius equal to 1. Thanks to the teleportation factor, $G$ is strictly positive and hence irreducible (and also primitive). Hence, by Perron-Frobenius theorem, a normalized and strictly positive PageRank vector exists and is unique. It is the left-hand dominant eigenvector of the Google matrix $G$, that is, the left-hand eigenvector associated with the eigenvalue of largest absolute value.
We can arrive at the same result using Markov processes. The stochastic matrix $G$ can be interpreted as the transition matrix of a Markov chain on a finite set of states. Since $G$ is primitive, the Markov theorem applies, and the PageRank vector $\pi$ corresponds to the unique stationary distribution of the Markov chain.
A last crucial question remains: how fast is the computation of the PageRank vector? The success of PageRank is largely due to the existence of a fast method to compute its values: the power method. The power method is one of the oldest and simplest methods for finding the dominant eigenpair of a matrix. With respect to the Google matrix $G$, it works as follows: let $\pi^{(0)} = v$ be an arbitrary starting vector. Repeatedly compute:
$\pi^{(k+1)} = \pi^{(k)} G
until $||\pi^{(k+1)} - \pi^{(k)}||_1 < \epsilon$, where the norm-1 $||\cdot||_1$ measures the distance between the two successive PageRank vectors and $\epsilon$ is the desired precision.
There are several good reasons to choose the power method to solve the PageRank problem. First, it is simple and elementarily implementable. Moreover, the power method applied to matrix $G$ can be easily expressed in terms of matrix $H$, which, unlike $G$, is a very sparse matrix. Matrix $H$ can be stored using a linear amount of memory and the vector-matrix multiplication $\pi H$ has linear complexity. Finally, the power method converges after a remarkably short number of steps.
In fact, the balancing parameter $\alpha$ governs the speed of convergence of the method. The asymptotic rate of convergence of the power method depends on the ratio of the two eigenvalues of $G$ that are largest in magnitude, denoted $\lambda_1$ and $\lambda_2$. Specifically, it is the rate at which $|\lambda_2 / \lambda_1|^k$ goes to 0, where $k$ is the number of iterations of the power method. Since $G$ is stochastic, $\lambda_1 = 1$, so $|\lambda_2|$ governs the convergence. It turns out that $\lambda_2 = \alpha \mu_2$, where $\mu_2$ is the subdominant eigenvalue of $S$. Since experiments have shown that the Web has a bow-tie structure fragmented into four main continents that are not mutually reachable, we assume that $\mu_2$ is close to 1. Indeed, stochastic matrices having a subdominant eigenvalue near to 1 are those whose states form clusters such that the states within each cluster are strongly linked to each other, but the clusters themselves are only weakly linked. Therefore the convergence rate is approximately $\alpha^k$. This means that to produce scores with $\tau$ digits of precision we must have $10^{-\tau} = \alpha^k$ and thus about $k = -\tau / \log_{10} \alpha$ iterations must be completed. For instance, if $\alpha = 0.85$, as many as 43 iterations are sufficient to gain 3 digits of accuracy and 142 iterations are enough for 10 digits of accuracy.
The balancing parameter $\alpha$ also determines the sensitivity of the PageRank vector to changes in the components of the PageRank model. Such components are the parameter $\alpha$ itself, the hyperlink matrix $H$, and the bookmark vector $b$. High sensitivity means that small changes in one of the components have large effects in the PageRank vector. Assuming a clustered Web, it turns out that, when $\alpha$ is small, PageRank is insensitive to slight variations in the PageRank model components. However, as $\alpha$ approaches 1, PageRank becomes increasingly sensitive to small perturbations in the PageRank components, and hence the PageRank outcome is less robust.
All in all, a balancing act is necessary when choosing the actual value of $\alpha$. Large values of $\alpha$ give more weight to the true link structure of the Web, but they slow down convergence of the power method and augment sensibility of the solution to changes in the model. On the other hand, small values of $\alpha$ make the PageRank method more efficient and robust, but the downside of using them is the higher influence of the artificial teleportation matrix.
What about if the Web were a random world instead? What would be the consequences for the performance of the power method computing PageRank scores and for the sensibility of PageRank vector? We conjecture that the subdominant eigenvalue of matrix $S$ for random graphs is significantly lower than 1. This would make the power method faster to converge and the PageRank vector more robust to changes in the structure of the problem. This means that we could increase the balancing parameter $\alpha$ giving more weight to the true structure of the Web. Preliminary experimental results confirm this hypothesis.
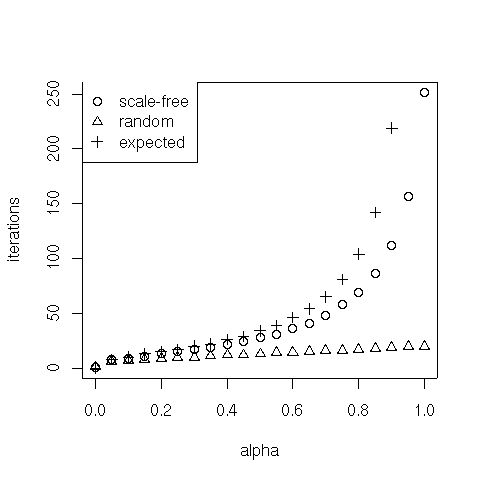
The following plot compares the convergence speed of the power method on a scale-free graph with power law node degree distribution and on a random graph with Poisson node degree distribution varying the parameter $\alpha$ uniformly. We also plot the expected speed assuming the subdominant eigenvalue of $S$ is equal to 1. As soon as the topology of the graph becomes important, that is for larger values of $\alpha$, the difference in computation speed between scale-free and random graphs is quite evident, while the scale-free convergence speed is close to the expected one.
The following chart plots the PageRank vectors varying the parameter $\alpha$ uniformly on a random graph. The vectors are sorted in increasing order.
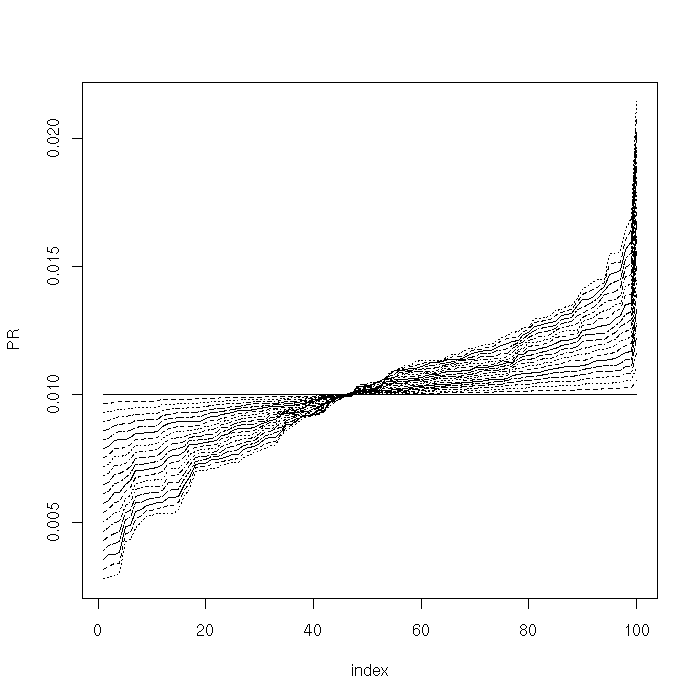
Compare with the same chart on a scale-free graph. For larger values of $\alpha$, the PageRank scores, in particular those for the most important nodes of the network, significantly vary as $\alpha$ slightly changes.
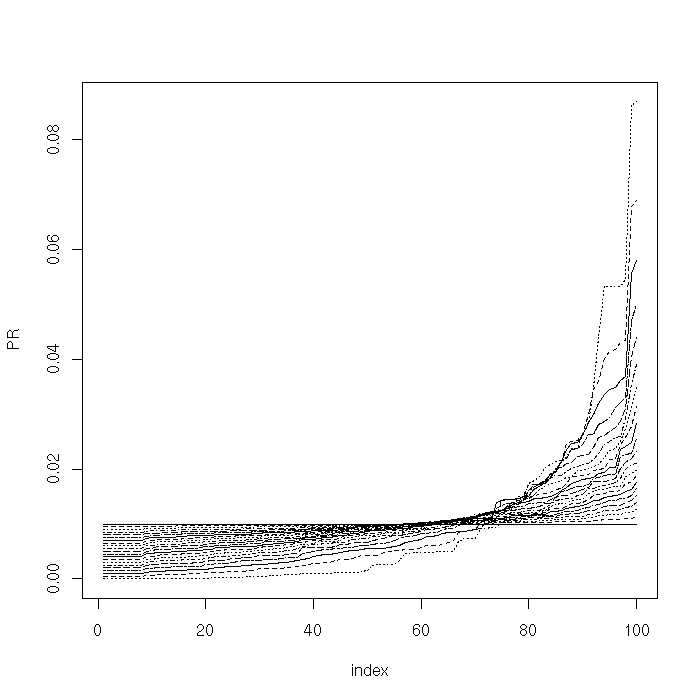
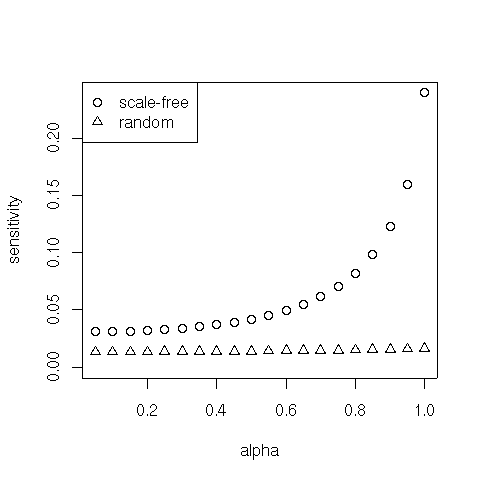
We finally plot (norm 1) distance between the computed PageRank vectors for different values of $\alpha$ on both types of graphs. As conjectured, the PageRank vector is more robust on random networks.