In this part we will learn to visualize a network. The code that we will use is based on the book Generative Design. We will use a visualization algorithm called force-directed. The idea of this algorithm is the following:
The sum of these two forces allows to obtain a visualization that draws close together nodes connected by edges. The idea is that nodes connected by an edge are similar to each other and groups of similar nodes are displayed in the same space.
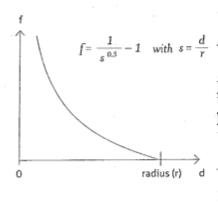
The first thing to calculate is the force of attraction between two nodes. The repulsion is then obtained as a negative attraction. Consider two moving nodes; one of them is an attractor and exerts a force of attraction on the other node by changing its movement. The force of attraction $f$ between two nodes acts within a radius $r$ of attraction and depends inversely on the distance $d$ between the nodes, that is if $d$ is small (close to 0) then the force $f$ is great, and if $d$ is great (close to $r$) then the force $f$ is small. Finally, the force is null when $d \geq r$. We can model the force of attraction with this formula: $$f = \frac{\sqrt{r} - \sqrt{d}}{\sqrt{d}} $$ assuming that $f = 0$ if $d \geq r$. Note that in this model the dependence is inverse of the square root of the distance; in the law of universal gravitation of Isaac Newton force depends instead by the inverse square of the distance.

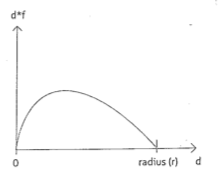
We can apply the force of attraction to the node that is attracted in this way. Each node is equipped with a motion vector (which indicates the speed and direction of motion). The force, calculated as above, is first multiplied by the vector distance between the two nodes involved, namely the difference vector between the two nodes, obtaining an attraction vector. Note that: $$d \cdot f = \sqrt{d} (\sqrt{r} - \sqrt{d})$$ The product $ d \cdot f $ is small when the distance is small or when the distance is close to the attraction radius $ r $, while it is large when the distance is in an intermediate position.
We can then add the attraction vector to the node movement vector:
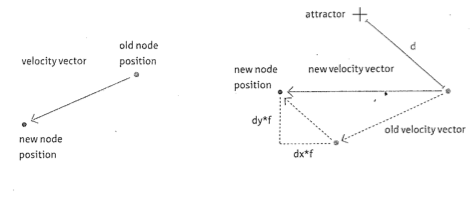
Finally, a repulsion force is obtained by changing the sign of the attraction vector. See the class Node in the downloaded code.
The force of attraction between two nodes connected by an edge is computed in this way. Imagine an edge as a spring with a distance at rest equal to $l$. If the two nodes are located more or less distant than $l$, then they will move trying to bring to this distance, approaching if the distance is greater than $l$ or moving away in the opposite case. The application of the force of attraction between the two connected nodes is schematized in the following way:
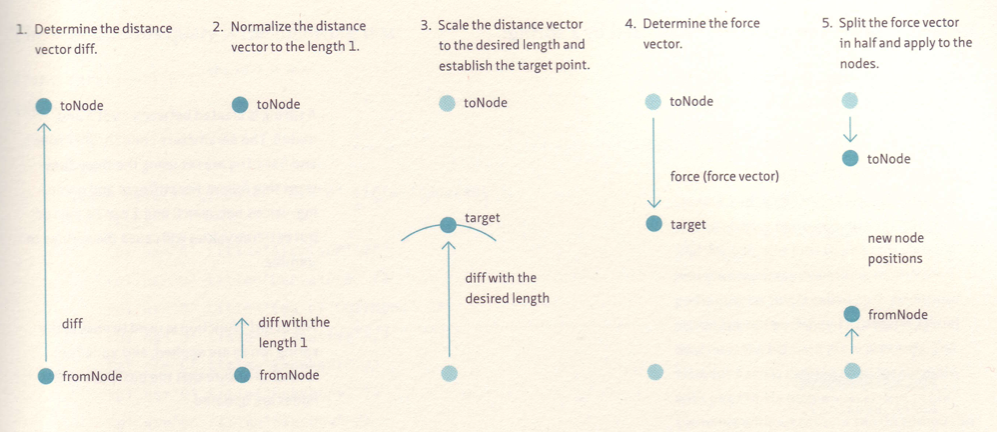
See class Spring in the downloaded code. Finally, we put together the attraction and repulsion forces in order to visualize the network. See sketch network in the downloaded code.