Native XML databases

Much information around in these days is semistructured, hierarchical, and hybrid in nature.

Semistructured data has a loose structure (schema): a core of attributes are shared by all objects associated with a semistructured schema, but many individual variants are possible. For instance, consider a bibliography containing references to academic publications. All references have in common a small core of attributes, like authors, title, and publication year. Different reference types, however, have many specific attributes. For instance, books have publishers, journal papers have volume numbers, conference contributions have titles of the proceedings and conference addresses, and theses have hosting institutes. Moreover, some of these attributes might be structured in different ways. For example, we might specify the name of an author as a unique token or as an arbitrarily long list of tokens, including space for possibly multiple first, middle, and last name components.

Hierarchical data is composed of atomic elements and compound elements. Atomic elements have a simple flat content. By contrast, compound elements contain nested sub-elements, either atomic or compound. There is no limit to the nesting level of information. The resulting structure is a hierarchy of information, possibly representable as a tree of objects. For instance, a Web page written in XHTML has a hierarchical structure in which tag elements might contain other tag elements. As another example, consider the biological taxonomic hierarchy in which a species, the most basic rank, nests inside a genus, which in turn nests inside a family, and so on.

The term hybrid data refers to the fact that information often mixes both data and text alike. For instance, a bibliographic reference might contain records, such as authors, title, year, as well as narrative information, like the paper abstract. Similarly, objects representing people in a social network mix attributes, like name and occupation, with possibly long and structured descriptions, like a CV.

Many researchers have proposed XML as the most appropriate formalism to work with this kind of information. XML has the following unique strengths as a data format:

Simple syntax. XML is a well-defined format whose documents are easy to create, manipulate, parse by computer software, and read by humans equipped with a basic text editor. Moreover, XML is portable across different computer architectures and programming languages;
Semistructured data. The flexibility of the XML data model allows one to represent unstructured information as well as data with a loose schema;
Support for nesting. The hierarchical nature of XML makes it possible to represent complex structures in a natural way;
Support for hybrid information. Both data-centric and text-centric information can be easily represented within the same XML document.

An XML database is a data persistence system that allows one to manage data in XML format. It must ensure those features of a traditional database system that are vital for real-world applications, including a universal, efficient, and scalable query language, data integrity constraints, transaction management, data privacy, backup, and recovery. Two major classes of XML databases exist:

XML-enabled databases. These systems map XML data to a traditional database, typically a relational database. XML data can be stored in different manners: an XML document can be shredded into relational fields, records and tables, it can be entirely stored as character data in records, or it can be saved as external character large objects.
Native XML databases. A native XML database defines a logical model for an XML document, and it stores and retrieves documents according to that method. Examples of such models are the XPath data model, the XML Infoset, and the models underlying DOM and SAX.

A notable example of XML database, implementing most of the mentioned features, is BaseX.

Unlike XML, the relational model allows one to store information in a structured and flat fashion. It follows that even simple and highly-related information, like an invoice with date and number accompanied by a list of invoice items (each one with description, quantity, and price attributes), must be spanned over multiple tables and potentially expensive queries, joining the scattered information through the key and foreign key mechanisms, must be used to reconstruct information at query time.

When is an XML database a better solution to a relational database? There is no clear answer. However, Ronald Bourret gives the following heuristic rule:

If you find yourself essentially building a relational database inside your native XML database, you might ask yourself why you aren't using a relational database in the first place.

The design of a database follows a consolidated methodology comprising conceptual, logical, and physical modeling of the data. In the following we give a contribution toward the development of design methodologies and tools for native XML databases. We adopt the well-understood Entity Relationship model, extended with specialization (ER for short), as the conceptual model for native XML databases. Moreover, we choose W3C XML Schema Language (XML Schema, hereinafter), as the schema language for XML. We propose a mapping from ER to XML Schema with the following properties: information and integrity constraints of the ER model are preserved, no redundancy is introduced, different hierarchical views of the conceptual information are permitted, the resulting structure is highly connected, and the design is reversible.

Representing XML Schema using its own syntax requires substantial space and the reader (and sometimes the developer as well) gets lost in the implementation details. We embed ER schemas into a more succinct target schema language for XML documents called XML Schema Notation (XSN for short) whose expressive power lies between DTD and XML Schema. XSN allows sequences and choices as in DTD. For instance:

the sequence definition author(name, surname) specifies an element author with two child elements name and surname;
the choice definition contact(phone | email) specifies that the element contact has exactly one child element either phone or email.

The sequence and choice operators can be combined and nested, as in author(((name, surname) | id), affiliation) which specifies that an author is described either by name, surname, and affiliation or by id and affiliation.

XSN extends DTD with the following three constructs:

occurrence constraints. These constrain the minimum and maximum number of occurrences of an item. The minimum constraint is a natural number and the maximum constraint is a natural number or the constant N denoting a finite unbounded natural number. The notation is item[x,y], where x is the minimum constraint, y is the maximum constraint, and item is a single element, a sequence, or a choice. We condiser the following shortcuts:
- when both x and y are equal to 1, the occurrence constraints may be omitted. That is, the definition item equals item[1,1];
- when x = 0 and y = 1, the occurrence constraints may be abbreviated as ?. That is, the definition item? equals item[0,1];
- when x = 0 and y = N, the occurrence constraints may be abbreviated as *. That is, the definition item* equals item[0,N];
- when x = 1 and y = N, the occurrence constraints may be abbreviated as +. That is, the definition item+ equals item[1,N];
key constraints. If A is an element and KA is a child element of A, then the notation KEY(A.KA) means that KA is a key for element A. Keys composed of more than one element are allowed; for instance, in KEY(A.K₁, A.K₂) the pair (K₁, K₂) is a key for element A. Moreover, it is possible to define keys over the union of different elements: the constraint KEY(A₁.K | A₂.K | ... | A_n.K) means that the element K must be unique over the union of the domains identified by the elements A₁ ... A_n.
foreign key constraints. If A is an element with key KA, B is an element, and FKA is a child element of B, then KEYREF(B.FKA --> A.KA) means that FKA is a foreign key of B referring to the key KA of A.

In key and keyref definitions, if A.KA is ambiguous, that is, if there exists another element A with a child element KA in the database, then a path to A can be specified as follows: A₁.A₂. ... .A_n.A.KA.

For the sake of simplicity, all information is encoded using XML elements and the use of XML attributes is avoided. The mapping of XSN into W3C XML Schema is achieved as follows: sequence and choice constructs correspond to sequence and choice schema elements; occurrence constraints are implemented with minOccurs and maxOccurs schema attributes; key and foreign key constraints are captured by key and keyref schema elements, respectively.

As an example of XSN definition, suppose we want to specify that a bibliography contains authors and papers. An author has a name and possibly an affiliation. An affiliation is composed of an institute and an address. A paper has one or more authors, a title, a publication source and year. Moreover, name is the key for element author, title is the key for element paper, and the author child element of paper is a foreign key referring to the name child element of author. We can specify this information in the following concise definition in XSL:

bibliography((author | paper)*)
  author(name, affiliation?)
    affiliation(institute, address)
  paper(author+, title, source, year)
KEY(author.name)
KEY(paper.title)
KEYREF(paper.author --> author.name)

An ER schema contains entities and relationships between entities. Both can have attributes, which can be either simple, composed, or multi-valued. Some entities are weak and are identified by proprietary entities through identifying relationships. Moreover, some entities may be specialized into more specific entities. Specializations may be either partial or total and either disjoint or overlapping. Relationships may involve two or more entities; each entity participates in a relationship with a minimum and a maximum participation constraint. The mapping from ER to XML Schema is as follows.

The database element

As a first step in the translation, we create a database element. This is a container for all unnested entity elements of the schema and corresponds to the document element in an XML instance of the schema. It is defined as an unbounded choice among all unnested entity elements. An instance is the bibliography element in the bibliographic example above.

Entities

Each entity is mapped to an element with the same name. Entity attributes are mapped to child elements (or attributes). The encoding of composed and multi-valued attributes takes advantage of the flexibility of the XML data model: composed attributes are translated by embedding the sub-attribute elements into the composed attribute element; multi-valued attributes are encoded using suitable occurrence constraints. As opposed to the relational mapping, no restructuring of the schema is necessary. An example is given below.

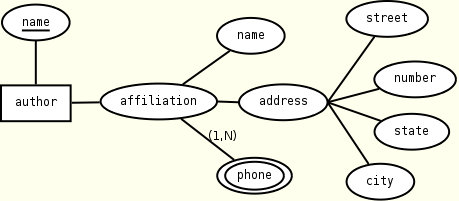
author(name, affiliation)
  affiliation(name, address, phone+)
    address(street, number, city, state)
KEY(author.name)

Relationships

Let us consider two entities A, with key KA, and B, with key KB, and a binary relation R between A and B. The encodings for all the typical cases are given in the following:

One-to-one relationships

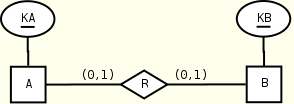
A(KA, R?)                          B(KB, R?)
 R(KB)                              R(KA)
B(KB)                              A(KA)
KEY(A.KA), KEY(B.KB), KEY(R.KB)    KEY(B.KB), KEY(A.KA), KEY(R.KA)
KEYREF(R.KB --> B.KB)              KEYREF(R.KA --> A.KA)

The two mappings (left and right) are equivalent in terms of number of used constraints. Notice that the constraint KEY(R.KB) is used to capture the right maximum participation constraint in the left mapping: it forces the elements KB of R to be unique, that is, each B element is assigned to at most one A element by the relation R. Similarly for the constraint KEY(R.KA) in the right solution. If relationship R has attributes, these are included in the element R that represents the relationship.

A(KA, R?)                     B(KB, R)
 R(B)                          R(KA)
  B(KB)                       A(KA)
KEY(A.KA), KEY(B.KB)          KEY(B.KB), KEY(A.KA), KEY(R.KA)
                              KEYREF(R.KA --> A.KA)

The suggested view is the left one. The element B is fully embedded into element A; hence no foreign key constraint is necessary and the right minimum cardinality holds by construction. The right maximum cardinality is captured by KEY(B.KB). The solution given on the right uses an additional key constraint for the left maximum cardinality as well as an extra foreign key constraint; moreover, it looses the chance to nest the resulting structure. Notice that the embedding is not possible whenever the right minimum constraint is 0 (as in the above case). Embedding in this case would lead to the loss of all B elements that are not associated with any A element. The embedding is neither possible whenever the right maximum constraint is greater than 1. Embedding in this case would introduce data redundancy and would violate the key constraint KEY(B.KB).

A(KA, R)                        B(KB, R)
 R(B)                            R(A)
  B(KB)                           A(KA)
KEY(A.KA), KEY(B.KB)            KEY(B.KB), KEY(A.KA)

The two symmetrical views are equivalent. An additional flat encoding is possible but not suggested:

A(KA, R)                      
 R(KB)                         
B(KB)                          
KEY(A.KA), KEY(B.KB), KEY(R.KB)           
KEYREF(R.KB --> B.KB), KEYREF(B.KB --> R.KB)

The right maximum constraint is coded with KEY(R.KB), while foreign key constraint KEYREF(B.KB --> R.KB) is used to capture the right minimum constraint. The latter claims that each B element must appear inside an R element of A, that is, each B element must be associated with at least one A element, implementing the mentioned constraint. Notice that this foreign key constraint is possible since R.KB is a key (in XML Schema, we cannot point a foreign key to something that is not a key).

One-to-many relationships

A(KA, R?)                      B(KB, R*)
 R(KB)                          R(KA)
B(KB)                          A(KA)
KEY(A.KA), KEY(B.KB)           KEY(B.KB), KEY(A.KA), KEY(R.KA)
KEYREF(R.KB --> B.KB)          KEYREF(R.KA --> A.KA)

The preferred mapping is shown on the left. The solution on the right uses an extra constraint to capture the left maximum cardinality.

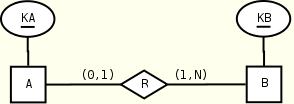
A(KA, R?)                          B(KB, R+)
 R(KB)                               R(KA)
B(KB)                              A(KA)   
KEY(A.KA), KEY(B.KB)               KEY(B.KB), KEY(A.KA), KEY(R.KA)
KEYREF(R.KB --> B.KB)              KEYREF(R.KA --> A.KA)
CHECK("right min")

The suggested mapping is given on the right. The constraint KEY(R.KA) is used to capture the left maximum cardinality. The opposite solution misses the encoding of the right minimum cardinality, which must be dealt with as an external constraint (added with clause CHECK). One may be tempted to add, in the left case, the foreign key KEYREF(B.KB --> R.KB) to check the missing constraint. The foreign key would force each B instance to be associated with at least one A instance. Unfortunately, such a foreign key is allowed in XML Schema only if R.KB is a key. However, R.KB cannot be a key since a B instance may be associated with more than one A instance and hence there may exist repeated B instances under A, a situation that clearly violates the key constraint.

A(KA, R)                         B(KB, R*)
 R(KB)                            R(A) 
B(KB)                              A(KA)
KEY(A.KA), KEY(B.KB)             KEY(B.KB), KEY(A.KA) 
KEYREF(R.KB --> B.KB)

The best solution is the right one that uses the full nesting of elements. The opposite embedding, on the left, spends an extra keyref constraint and does not achieve element nesting.

A(KA, R)                             B(KB, R+)  
 R(KB)                                R(A)  
B(KB)                                  A(KA)
KEY(A.KA), KEY(B.KB)                 KEY(B.KB), KEY(A.KA) 
KEYREF(R.KB --> B.KB)
CHECK("right min")

The preferred mapping is the one given on the right. The opposite embedding fails to capture the right minimum cardinality and uses an additional foreign key constraint.

Many-to-many relationships

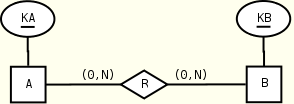
A(KA, R*)                      B(KB, R*)
 R(KB)                          R(KA)
B(KB)                          A(KA)
KEY(A.KA), KEY(B.KB)           KEY(B.KB), KEY(A.KA)
KEYREF(R.KB --> B.KB)          KEYREF(R.KA --> A.KA)

The two symmetrical views use the same number of constraints.

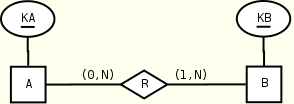
A(KA, R*)                         B(KB, R+)
 R(KB)                             R(KA)  
B(KB)                             A(KA) 
KEY(A.KA), KEY(B.KB)              KEY(B.KB), KEY(A.KA) 
KEYREF(R.KB --> B.KB)             KEYREF(R.KA --> A.KA)
CHECK("right min")

The mapping on the right is the one we propose. The opposite embedding looses the right minimum participation constraint.

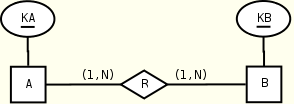
A(KA, R+)                              B(KB, R+)
 R(KB)                                  R(KA)
B(KB)                                  A(KA)
KEY(A.KA), KEY(B.KB)                   KEY(B.KB), KEY(A.KA)
KEYREF(R.KB --> B.KB)                  KEYREF(R.KA --> A.KA)
CHECK("right min")                     CHECK("left min")

Notice the use of an external constraint in both solutions to check the minimum participation constraint: this is the only case in the mapping of relationships in which we have to resort to external constraints in the preferred mapping.

An alternative bi-directional solution is the one that pairs the two described mappings, that is:

A(KA, R1+)
 R1(KB)
B(KB, R2+)
 R2(KA)
KEY(A.KA), KEY(B.KB)  
KEYREF(R1.KB --> B.KB)
KEYREF(R2.KA --> A.KA)
CHECK("inverse relationship")

Such a solution captures all integrity constraints specified at conceptual level. It imposes, however, the verification of an additional inverse relationship constraint, namely, if an instance x of A is inside an instance y of B, then y must be inside x in the inverse relationship. Such a constraint is not expressible in XML Schema.

It is interesting to notice that, thanks to its hierarchical nature, the XML logical model allows to capture more constraints specified at conceptual level than the relational logical model. Indeed, for all relationships with one participation constraint equal to (1,N), the minimum participation constraint is lost when mapping the ER model into the relational model.

Weak entities

A weak entity always participates in the identifying relationship with participation constraint equal to (1,1). Hence, depending on the form of the second participation constraint, one of the cases discussed above applies. The key of the weak entity is obtained by composing its partial key with the key of the owner entity and the owner key in the weak entity must match the corresponding key in the owner entity.

A(KA, R*)
 R(B)
  B(KB, KA)
KEY(A.KA), KEY(B.KB, B.KA)
CHECK(B.KA = A.KA)

The external constraint CHECK(B.KA = A.KA) cannot be avoided. Indeed, suppose we remove the owner key KA from the weak entity B as done above:

A(KA, R*)
 R(B)
  B(KB)
KEY(A.KA), KEY(B.KB, A.KA)

Unfortunately, the key constraint KEY(B.KB, A.KA) is no more expressible in XML Schema: if we point the selector of the key schema element at the level of entity A, then the field pointing to KB is invalid since it selects more than one node (A may be associated with more than one B element in this case); on the other hand, if we point the selector at the level of entity B, then the field referring to KA is also not valid, since it must use the parent or ancestor axes to ascend the tree, but such axes are not admitted in the XPath subset supported by W3C XML Schema.

Specialization

The mapping fully exploits the hierarchical nature of the XML data model. Consider the following example:

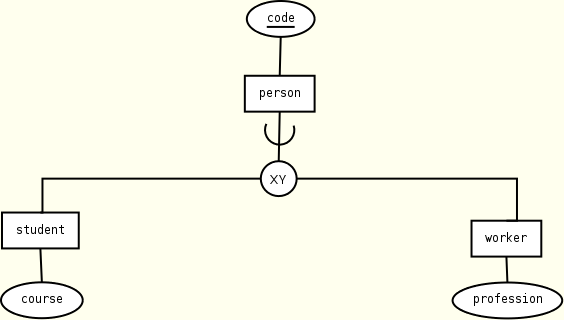
If the specialization is partial-overlapping, then the mapping is as follows:

person(code, student?, worker?)
  student(course)
  worker(profession)
KEY(person.code)

Both student and worker elements are embedded inside person element. Neither key nor foreign key constraints are necessary. The partial-overlapping constraint is captured by using the occurrence specifiers. As an alternative we have the following more elaborated flat solution:

person(code)
student(code, course)
worker(code, profession)
KEY(person.code), KEY(student.code), KEY(worker.code)
KEYREF(student.code --> person.code)
KEYREF(worker.code --> person.code)

If the specialization is total-overlapping, the mapping is as follows:

person(code, ((student, worker?) | worker))
  student(course)
  worker(profession)
KEY(person.code)

Notice that the above schema is deterministic. As an alternative we have the following solution:

student(code, course)
worker(code, profession)
KEY(student.code), KEY(worker.code)

In case of partial-disjoint specialization we have the following encoding:

person(code, (student | worker)?)
  student(course)
  worker(profession)
KEY(person.code)

An alternative flat solution follows:

person(code)
student(code, course)
worker(code, profession)
KEY(person.code), KEY(student.code | worker.code)
KEYREF(student.code --> person.code)
KEYREF(worker.code --> person.code)

Notice the key constraint KEY(student.code | worker.code) that forces disjointness: the code value must be unique across both student and worker elements. Finally, a total-disjoint specialization in encoded as follows:

person(code, (student | worker))
  student(course)
  worker(profession)
KEY(person.code)

The alternative flat solution follows:

student(code, course)
worker(code, profession)
KEY(student.code | worker.code)

Once again the XML logical model allows to capture more constraints specified at conceptual level than the relational logical model. Indeed, some specialization constraints are lost when mapping to the relational model.

As a full example of the mapping, consider the following ER schema which describes a citation-enhanced bibliography, a typical semi-structured data application.

publication(title, year, citations, reference*, 
            authorship+, (article | book)?)
  reference(title)
  authorship(name, contribution)
  article(pages, abstract, (journal | conference))
    journal(name, volume)
    conference(name, place)
  book(ISBN)
publisher(name, address, publishing+)
  publishing(title)
author(name, affiliation+)
  affiliation(institute, address)

KEY(publication.title) 
KEY(publisher.name)
KEY(author.name) 
KEY(publishing.title)
KEYREF(reference.title --> publication.title)
KEYREF(authorship.name --> author.name)
KEYREF(publishing.title --> publication.title)

Here are the XML Schema version of the above schema and a sample XML document valid with respect to the defined schema.

Nesting the XML structure

Nesting the XML structure has two advantages. The first advantage is the reduction of the number of constraints inserted in the mapped schema and hence of the validation overhead. The second advantage is the decrease of the (expensive) join operations needed to reconstruct the information at query time. Indeed, highly nested XML documents can be better exploited by tree-traversing XML query languages like XPath.

We illustrate these points with the following example. Suppose we want to model a one-to-one relationship direction between entities manager (man) and department (dep):

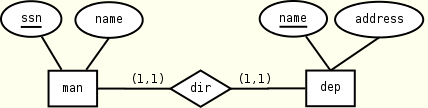
In the following, we propose a flat mapping (on the left) and a nested mapping (on the right) of the ER fragment:

man(ssn, name, dir)                  man(ssn, name, dir)
  dir(name)                           dir(dep)
dep(name, address)                     dep(name, address)
KEY(man.ssn)                         KEY(man.ssn)
KEY(dep.name)                        KEY(dep.name)
KEY(dir.name)
KEYREF(dep.name  --> dir.name)
KEYREF(dir.name --> dep.name)

Notice that nesting saves three constraints over five (one key and two foreign keys). Furthermore, suppose we want to retrieve the address of the department directed by William Strunk. A first version of this query written in XPath and working over the flat schema follows:

/dep[name = /man[name = "William Strunk"]/dir/name]/address

The query joins, in the outer filter, the name of the current department and the name of the department directed by William Strunk. This amounts to jump from the current node to the tree root. An alternative XPath query tailored for the nested schema is given in the following:

/man[name = "William Strunk"]/dir/dep/address

This version of the query fluently traverses the tree without jumps. The same happens if the query is written in XQuery. We expect that the second version of the query is processed more efficiently by most XML query processors.

Suppose we want to find the names of the managers of the departments located in Italy. A solution on the flat schema necessarily uses a join:

/man[dir/name = /dep[contains(address, "Italy")]/name]/name

while the one on the nested schema avoids it by exploiting the parent axis:

/man/dir/dep[contains(address, "Italy")]/../../name