Soluzione Esercizio 4 dell'Esercitazione #11

Soluzione

Scriveremo il programma Esercizio11_4. Iniziamo quindi a scrivere nel file Esercizio11_4.java il seguente codice:

1. (*) Chiameremo triangolareInferiore il metodo che controlla se una matrice è triangolare inferiore.
   Una matrice viene detta triangolare inferiore quando tutti i suoi elementi sopra la diagonale sono uguali a zero, ovvero, tutti gli elementi m[i][j] quando i < j sono uguali a 0 (Figura 1).

   1 0 0 0
   2 3 0 0
   3 1 5 0
   2 5 3 1

   Figura 1. Una matrice triangolare inferiore
   Per controllare in modo ricorsivo che una matrice sia triangolare inferiore si può procedere in questo modo:
   1. caso base: una matrice di dimensione 1 è sempre triangolare inferiore, infatti, non essendoci elementi sopra la diagonale, non si riesce a trovare nessun elemento al di sopra della diagonale che sia diverso da zero e quindi la condizione non è violata;
   2. caso generale: una matrice di dimensione >1 sarà diagonale inferiore se la prima riga ha tutti gli elementi dopo quello sulla diagonale uguali a zero e se (questa è la chiamata ricorsiva) la sottomatrice che si ottiene eliminando la prima riga e la prima colonna è anch'essa diagonale inferiore (Figura 2).

      1 0 0 0    1 0 0 0
      2 3 0 0    2 3 0 0
      3 1 5 0    3 1 5 0
      2 5 3 1    2 5 3 1

      Figura 2. Una matrice è triangolare inferiore se la prima riga ha tutti zeri dopo la diagonale e se la sottomatrice è triangolare inferiore.
      Il metodo triangolareInferiore dovrà restituire un boolean e avrà un parametro m di tipo int[][].
      Invece di far costruire per ogni chiamata ricorsiva la sottomatrice, per risparmiare tempo e spazio possiamo aggiungere un parametro che indichi al metodo quale riga stiamo controllando. Con questo trucco simuliamo la chiamata ricorsiva su una sottomatrice facendo invece una chiamata ricorsiva sulla stessa matrice, ma sulla riga successiva.
      Per "nascondere" all'utente questo trucco scriveremo un metodo private con i due parametri, mentre lasceremo quello public con un solo parametro. Il suo codice sarà:
      public static boolean triangolareInferiore(int[][] m) {
        return triangolareInferiore(m,0);
      }
      Il metodo private, che fa tutto il lavoro, sarà:
      private static boolean triangolareInferiore(int[][] m, int r) {
        boolean triangolare;
        if (r < m.length-1) {
        //non siamo ancora arrivati all'ultima riga
          triangolare = ...//controlla che tutti gli elementi
                           //dopo la diagonale siano == a zero
          triangolare = triangolare && triangolareInferiore(m,r+1)); //chiamata ricorsiva
        } else
          triangolare = true; //caso base
        return triangolare;
      }
      Al posto dei puntini conviene scrivere un metodo (anch'esso private) che controlli se gli elementi di una riga di una matrice sono tutti zero da un certo indice in poi. Visto che una riga di una matrice è un array, il metodo avrà intestazione
      private static boolean tuttiZeri(int[] a, int i)
      Possiamo definire anche questo metodo in modo ricorsivo pensando che
      1. caso base: un array a ha sicuramente tutti gli elementi dopo l'indice i uguali a zero quando l'indice è più grande della lunghezza dell'array;
      2. caso generale: un array a ha tutti gli elementi dopo l'indice i uguali a zero se a[i] è uguale a zero e se (questa è la chiamata ricorsiva) ha tutti gli elementi dopo l'indice i+1 uguali a zero.
      Il codice di tuttiZeri sarà:
      private static boolean tuttiZeri(int[] a, int i) {
        boolean zeri;
         if (i < a.length) {
         //caso generale
           zeri = (a[i] == 0);
           zeri = zeri & tuttiZeri(a,i+1); //chiamata ricorsiva
         } else
         //caso base
           zeri = true;
         return zeri;
      }
      Notate che tuttiZeri ritorna true se i≥a.length oppure se a[i]==0 e tuttiZeri(a,i+1). Questo può essere espresso dalla seguente espressione:
      (i >= a.length) || ((a[i] == 0) && tuttiZeri(a,i+1))
      e quindi il codice di tuttiZeri può essere riscritto in modo più elegante ed efficiente in questo modo:
      private static boolean tuttiZeri(int[ ] a, int i) {
         return (i >= a.length) || ((a[i] == 0) && tuttiZeri(a,i+1));
      }
      Bello vero? :-) (dite di sì così ci fate contenti...)
      Notate l'uso degli operatori condizionali || e && che valutano i due argomenti solo quando necessario. Per esempio, quando i ≥ a.length tutto il resto dell'espressione (((a[i] == 0) && tuttiZeri(a,i+1))) non verrà valutata. Se avessimo usato gli operatori logici | e & avremmo ottenuto un errore durante l'esecuzione perché non si può valutare a[i] quando i è maggiore di a.length-1.
      Dopo aver definito tuttiZeri possiamo completare triangolareInferiore:
      private static boolean triangolareInferiore(int[][] m, int r) {
         boolean triangolare;
         if (r < m.length-1) {
         //non siamo ancora arrivati all'ultima riga
           triangolare = tuttiZeri(m[r],r+1); //controlla che tutti gli elementi
                                             //dopo la diagonale siano == a zero
           triangolare = triangolare && triangolareInferiore(m,r+1)); //chiamata ricorsiva
         } else
           triangolare = true; //caso base
         return triangolare;
      }
      Anche in questo caso, come per tuttiZeri, possiamo riscrivere il codice in modo più elegante ed efficiente, considerando che una matrice è triangolare inferiore dalla riga r in poi se r>=m.length oppure se gli elementi della riga m[r] sono tuttiZeri da r+1 in poi e se la matrice è triangolareInferiore da r+1 in poi. L'espressione equivalente a quanto detto sopra è:
      (r >= m.length) || (tuttiZeri(m[r],r+1) && triangolareInferiore(m,r+1))
      e dunque triangolareInferiore può essere riscritto
      private static boolean triangolareInferiore(int[][] m, int r) {
        return (r >= m.length) || (tuttiZeri(m[r],r+1) && triangolareInferiore(m,r+1));
      }
      La versione iterativa triangolareInferioreIterativa(int[][] m) è molto simile. Basta fare un ciclo in cui si controlla che tutti gli elementi di una riga r sono zeri da r+1 in poi:
      public static boolean triangolareInferioreIterativa(int[][] m) {
        boolean triangolare = true;
         for (int r = 0; r<m.length; r++)
           triangolare = triangolare && tuttiZeri(m[r],r+1);
         return triangolare;
      }
      Il codice di Esercizio11_4 sarà:
      public class Esercizio11_4 {
      
         public static boolean triangolareInferiore(int[][] m) {
           return triangolareInferiore(m,0);
         }
      
         public static boolean triangolareInferioreIterativa(int[][] m) {
           boolean triangolare = true;
           for (int r = 0; r<m.length; r++)
             triangolare = triangolare && tuttiZeri(m[r],r+1);
           return triangolare;
         }
      
         private static boolean triangolareInferiore(int[][] m, int r) {
           return (r >= m.length) || (tuttiZeri(m[r],r+1) && triangolareInferiore(m,r+1));
         }
      
         private static boolean tuttiZeri(int[] a, int i) {
           return (i >= a.length) || ((a[i] == 0) && tuttiZeri(a,i+1));
         }
      
         public static void main(String[] args) {
           int[][] x = {{1,0,0,0},
                        {2,3,0,0},
                        {3,1,5,0},
                        {2,5,3,1}};
           int[][] y = {{1,0,0,3},
                        {2,3,0,0},
                        {3,1,5,0},
                        {2,5,3,1}};
           int[][] z = {{1,0,0,0},
                        {2,3,0,0},
                        {0,0,5,0},
                        {0,5,3,1}};
      
           System.out.println("x triangolare inferiore: " + triangolareInferiore(x));
           System.out.println("y triangolare inferiore: " + triangolareInferiore(y));
           System.out.println("z triangolare inferiore: " + triangolareInferiore(z));
         }
      }
2. Una matrice è triangolare se è triangolare superiore oppure triangolare inferiore. Avendo già definito i due metodi (triangolare superiore nell'esercizio 2 di questa stessa esercitazione), il metodo triangolare sarà molto semplice:
   public static boolean triangolare(int[][] m) {
     return triangolareInferiore(m) || Esercizio11_2.triangolareSuperiore(m);
   }
3. Una matrice è diagonale se è triangolare superiore e anche triangolare inferiore. Il metodo diagonale sarà quindi:
   public static boolean diagonale(int[][] m) {
     return triangolareInferiore(m) && Esercizio11_2.triangolareSuperiore(m);
   }
4. Per "fortuna" avevamo già definito il metodo tuttiZeri per scrivere efficientemente triangolareInferiore. Ora basterà dichiararlo public invece di private.
5. Un array a ha gli elementi da i a j uguali a zero se:
   1. caso base: se i è maggiore di j;
   2. caso generale: se a[i] è uguale a zero e, ricorsivamente, ha tutti gli elementi da i+1 a j uguali a zero.
   Il metodo ricorsivo tuttiZeri(int[] a, int i, int j) sarà quindi:
   public static boolean tuttiZeri(int[] a, int i, int j) {
     return (i > j) || (a[i]==0 && tuttiZeri(a,i+1,j));
   }
   Ora che abbiamo definito la versione più generale di tuttiZeri, potremmo riscrivere il codice dell'esercizio4.4 in questo modo:
   public static boolean tuttiZeri(int[] a, int i) {
     return tuttiZeri(a,i,a.length);
   }
   Tornando alla versione generale, il metodo iterativo invece ha un ciclo che controlla tutti gli elementi da i a j:
   public static boolean tuttiZeriIterativo(int[] a, int i, int j) {
     boolean zeri = true;
     for (int k = i; k <= j; k++)
       zeri = zeri && a[k] == 0;
     return zeri;
   }
   Il metodo precedente ha il difetto di controllare sempre tutti gli elementi da i a j. Questo non è molto efficiente: al primo elemento diverso da zero sappiamo che dovremo ritornare false anche senza controllare tutti i rimanenti. Per sfruttare questa osservazione possiamo riscrivere il metodo così:
   public static boolean tuttiZeriIterativo(int[] a, int i, int j) {
     int k = i;
     while (k <= j) {
       if (a[k] != 0) break;
       k++;
     }
     return (k > j);
   }
   L'istruzione if (a[k] != 0) break; fa terminare il ciclo appena si trova un elemento diverso da zero. Alla fine del ciclo se k > j vuol dire che il ciclo è stato completato oppure che i era maggiore di j e quindi il ciclo non è stato nemmeno iniziato. In entrambi i casi il metodo deve restituire true, altrimenti, se k è minore o uguale a j, vuol dire che si è incappati nel break, allora c'è almeno un elemento diverso da zero (per l'appunto a[k]) ed il metodo deve tornare false. Tutto quanto detto si traduce in
   if (k > j)
     return true;
   else
     return false;
   che è il modo sbagliato di scrivere l'istruzione equivalente (ma molto più leggibile ed elegante!)
   return (k > j)
   Notate che anche per triangolareInferioreIterativa valgono le stesse considerazioni, quindi il codice può essere riscritto nel modo seguente:
   public static boolean triangolareInferioreIterativa(int[][] m) {
     int r = 0;
      while (r < m.length) {
        if (!tuttiZeri(m[r],r+1)) break;
        r++;
     }
      return (r >= m.length);
   }
6. (*) La trasposta di una matrice si può ottenere in modo ricorsivo nel modo seguente:
   1. caso base: la trasposta di una matrice di dimensione 1 è la matrice stessa;
   2. caso generale: la trasposta di una matrice di dimensione maggiore di 1 si ottiene scabiando gli elementi della prima riga con quelli della prima colonna e poi trasponendo la sottomatrice (ormai avrete capito che questa è la chiamata ricorsiva...) che si ottiene eliminando la prima riga e la prima colonna.

   1 0 0 0    1 2 3 2
   2 3 0 0    0 3 0 0
   3 1 5 0    0 1 5 0
   2 5 3 1    0 5 3 1

   Figura 3. La matrice trasposta si ottiene scambiando gli elementi della prima riga con quelli della prima colonna e poi trasponendo la sottomatrice ottenuta togliendo la prima riga e la prima colonna.
   Analogamente a quanto abbiamo fatto con la versione ricorsiva di triangolareInferiore, simuleremo la chiamata sulla sottomatrice chiamando, ricorsivamente sulla stessa matrice, ma sulla riga successiva.
   Il metodo trasposta consisterà dunque nella sola chiamata al metodo private con parametro aggiuntivo la riga 0 da cui si deve partire per trasporre la matrice:
   public static int[][] trasposta(int[][] m) {
     return trasposta(m,0);
   }
   Il codice del metodo private sarà invece:
   private static int[][] trasposta(int[][] m, int i) {
     if (i >= m.length-1)
        return m;
      for (int j = i+1; j < m.length; j++) {
        int temp = m[i][j];
        m[i][j] = m[j][i];
        m[j][i] = temp;
      }
      return trasposta(m,i+1);
   }
   La versione iterativa fa un ciclo in cui scambia gli elementi della riga dopo la diagonale con quelli della colonna sotto la diagonale:
   public static int[][] traspostaIterativa(int[][] m) {
      for (int i = 0; i < m.length-1; i++)
        for (int j = i+1; j < m.length; j++) {
          int temp = m[i][j];
          m[i][j] = m[j][i];
          m[j][i] = temp;
        }
      return m;
   }
   Notate che il codice è praticamente lo stesso della versione ricorsiva a parte il cilo for più esterno. Notate anche che questa volta, a differenza delle altre, non si può spezzare prima il ciclo con un break perché per trasporre una matrice occorre scambiare tutti gli elementi fino all'ultimo.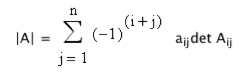
7. (*) Il determinante di una matrice di dimensione 1 è uguale al suo unico elemento. Il determinante di una matrice di dimensione maggiore si calcola in modo ricorsivo con la formula di Laplace
   
   Con Aij si indende il minore complementare di aij, cioè la matrice ottenuta da A togliendo la riga i e la colonna j.
   Quindi per calcolare il determinante di una matrice basta sommare i prodotti di tutti gli elementi di una riga qualsiasi (anche una colonna andrebbe bene) moltiplicati per i loro minori complementari cambiati di segno se la somma tra l'indice di riga e quello di colonna è dispari.
   Visto che va bene qualsiasi riga, possiamo prendere in cosiderazione la riga 0 e il codice del metodo determinante sarà:
   public static int determinante(int[][] m) {
     if (m.length < 2)
       return m[0][0];
     int somma = 0;
     for (int i = 0; i < m.length; i++)
       somma += m[0][i] * (i%2 == 0 ? 1 : -1) * determinante(minore(m,0,i));
     return somma;
   }
   Il metodo private int[][] minore che restituisce il minore complementare sarà:
   private static int[][] minore(int[][] m, int r, int c) {
     int[][] minore = new int[m.length-1][m.length-1];
     int rm = 0;
     for (int i = 0; i < m.length; i++) {
       int cm = 0;
       if (i != r) {
         for (int j = 0; j < m.length; j++)
           if (j != c)
             minore[rm][cm++] = m[i][j];
         rm++;
       }
     }
     return minore;
   }

Paolo Coppola
Last modified: 2003-03-17