A potential problem with Katz centrality is the following: if a node with high centrality links many others then all those others get high centrality. In many cases, however, it means less if a node is only one among many to be linked. The centrality gained by virtue of receiving a link from an important node should be diluted if the important vertex is very magnanimous with endorsements.
PageRank is an adjustment of Katz centrality that takes into consideration this issue. There are three distinct factors that determine the PageRank of a node: (i) the number of links it receives, (ii) the link propensity of the linkers, and (iii) the centrality of the linkers. The first factor is not surprising: the more links a node attracts, the more important it is perceived. Reasonably, the value of the endorsement depreciates proportionally to the number of links given out by the endorsing node: links coming from parsimonious nodes are worthier than those emanated by spendthrift ones. Finally, not all nodes are created equal: links from important vertices are more valuable than those from obscure ones. This method has been coined (and patented) by Sergey Brin and Larry Page (The anatomy of a large-scale hypertextual web search engine. Computer networks and ISDN systems, 1998). The PageRank thesis might be summarized as follows:
A node is important if it linked from other important and link parsimonious nodes or if it is highly linked.
Let $A = (a_{i,j})$ be the adjacency matrix of a directed graph. The PageRank centrality $x_{i}$ of node $i$ is given by: $$x_i = \alpha \sum_k \frac{a_{k,i}}{d_k} \, x_k + \beta$$ where $\alpha$ and $\beta$ are constants and $d_k$ is the out-degree of node $k$ if such degree is positive, or $d_k = 1$ if the out-degree of $k$ is null. In matrix form we have: $$x = \alpha x D^{-1}A + \beta$$ where $\beta$ is now a vector whose elements are all equal a given positive constant and $D^{-1}$ is a diagonal matrix with $i$-th diagonal element equal to $1/d_{i}$. Notice that, as seen for Katz centrality, PageRank is determined by an endogenous component that takes into consideration the network topology and by an exogenous component that is independent of the network structure. It follows that $x$ can be computed as: $$x = \beta (I - \alpha D^{-1}A)^{-1}$$
The damping factor $\alpha$ and the personalization vector $\beta$ have the same role seen for Katz centrality. In particular, $\alpha$ should be chosen between $0$ and $1 / \rho(D^{-1}A)$. Also, when the network is large, it is preferable to use the power method for the computation of PageRank.
A user-defined function pagerank.centrality using the solve R function follows:
# PageRank centrality
# INPUT
# g = graph
# alpha = damping factor
# beta = exogenous vector
pagerank.centrality = function(g, alpha, beta) {
n = vcount(g);
A = get.adjacency(g);
I = diag(1, n);
d = degree(g, mode="out");
d[d==0] = 1;
D = diag(1/d);
c = beta %*% solve(I - alpha * D %*% A);
return(as.vector(c));
}
An alternative user-defined function pagerank.centrality using a direct computation is the following:
# PageRank centrality (direct method)
# g = graph
# alpha = damping factor
# beta = exogenous vector
# t = precision
# OUTPUT
# A list with:
# vector = centrality vector
# iter = number of iterations
pagerank.centrality = function(g, alpha, beta, t) {
n = vcount(g);
A = get.adjacency(g);
d = degree(g, mode="out");
d[d==0] = 1;
D = diag(1/d);
A = D %*% A
x0 = rep(0, n);
x1 = rep(1/n, n);
eps = 1/10^t;
iter = 0;
while (sum(abs(x0 - x1)) > eps) {
x0 = x1;
x1 = alpha * x1 %*% A + beta;
iter = iter + 1;
}
return(list(vector = as.vector(x1), iter = iter))
}
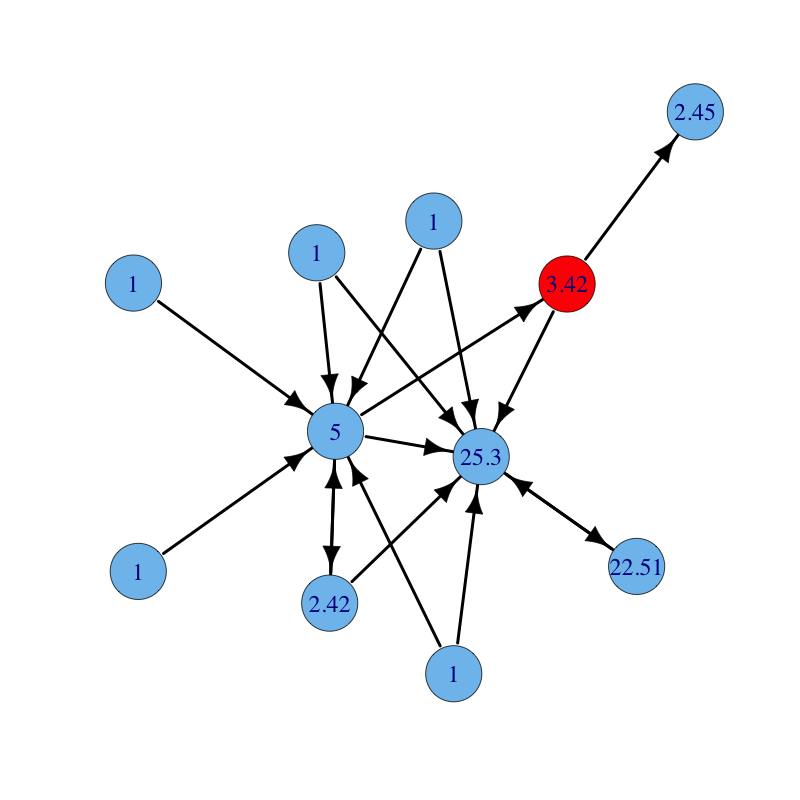
A directed graph with nodes labelled with their PageRank centrality ($\rho(D^{-1}A) = 1$). Parameters are: $\alpha = 0.85$ and $\beta = 1$:

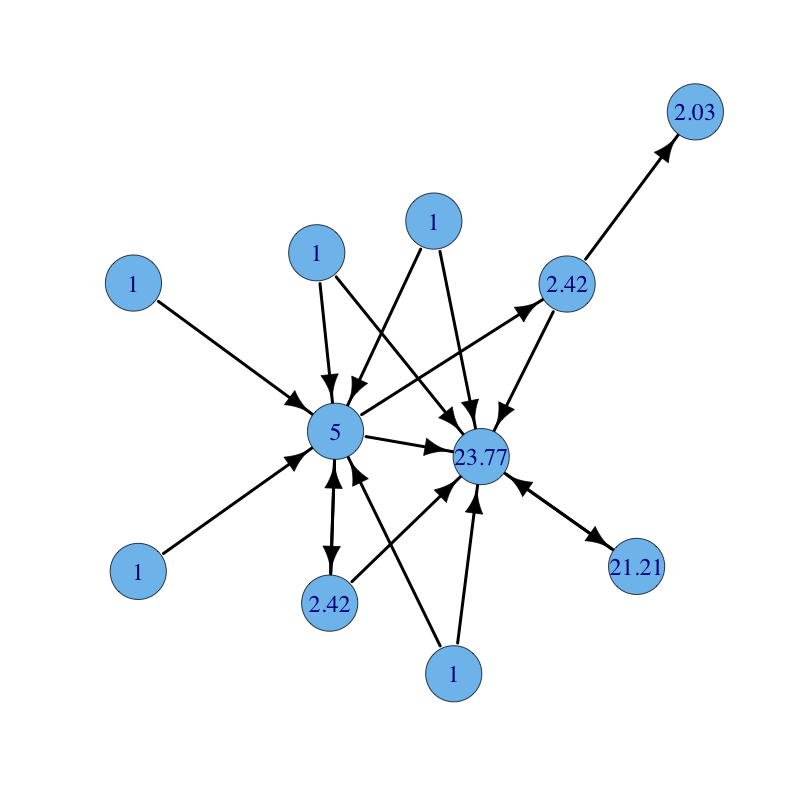
The same graph with parameters $\alpha = 0.85$ and $\beta = 1$ for all nodes but the red node for which $\beta = 2$ (notice how the red node and all nodes reachable from it increase their centrality):