So far, a node is important if it contains valuable content and hence receives many links from other important sources. Nodes with no incoming links cumulate, in the best case, only a minimum amount of centrality, regardless of how many other useful information sources they reference. One can argue that a node is important also because it links to other important vertices. For instance, a review paper may refer to other authoritative sources: it is important because it tells us where to find trustworthy information. Thus, there are now two types of central nodes: authorities, that contain reliable information on the topic of interest, and hubs, that tell us where to find authoritative information. A node may be both an authority and a hub: for instance, a review paper may be highly cited because it contains useful content and it may as well cite other useful sources. This method has been conceived by Jon M. Kleinberg (Authoritative sources in a hyperlinked environment. In ACM-SIAM Symposium on Discrete Algorithms, 1998). The Kleinberg centrality thesis reads:
A node is an authority if it is linked to by hubs; it is a hub if it links to authorities.
We can still add to Kleinberg centrality an exogenous, possibly personalized, factor (as in the Katz method) or normalize vertex centralities by the out-degrees of vertices that point to them (as in the PageRank method).
Let $A = (a_{i,j})$ be the adjacency matrix of a directed graph. The authority centrality $x_{i}$ of node $i$ is given by: $$x_i = \alpha \sum_k a_{k,i} \, y_k$$ and hub centrality $y_{i}$ of node $i$ is given by: $$y_i = \beta \sum_k a_{i,k} \, x_k$$ where $\alpha$ and $\beta$ are constants. In matrix form we have: $$\begin{array}{lcl} x & = & \alpha y A \\ y & = & \beta x A^T \\ \end{array}$$ or, combining the two: $$\begin{array}{lcl} \lambda x & = & x A^T A \\ \lambda y & = & y A A^T \\ \end{array}$$ where $\lambda = (\alpha \beta)^{-1}$. It turns out that authority matrix $C = A^T A$ and hub matrix $R = A A^T$ have the same eigenvalues.
Matrix $C$ is known as co-citation matrix in bibliometrics; its element $c_{i,j} = \sum_k a_{k,i} a_{k,j}$ is the number of common predecessors of nodes $i$ and $j$, and $c_{i,i}$ is the number of predecessors (the in-degree) of node $i$. Matrix $R$ is known as co-reference matrix in bibliometrics; its element $r_{i,j} = \sum_k a_{i,k} a_{j,k}$ is the number of common successors of nodes $i$ and $j$, and $r_{i,i}$ is the number of successors (the out-degree) of vertex $i$. This gives an alternative interpretation to authorities and hubs: a node is an authority if it is highly co-cited with other authorities; a node is a hub if it highly co-references with other hubs.
Notice moreover that $\lambda x A^T = x A^T A A^T$ and hence $x A^T$ is an eigenvector of the co-reference matrix $A A^T$ with the same eigenvalue $\lambda$. Hence, once computed the authority vector $x$, we can get the hub vector as $y = x A^T$, or, equivalently, the hub score of $i$ is the sum of authority scores of nodes linked to by $i$.
A user-defined function kleinberg.centrality using a direct computation is the following:
# Kleinberg centrality (direct method)
# INPUT
# g = graph
# t = number of digits of precision
# OUTPUT
# A list with:
# a = authority vector
# h = hub vector
# val = dominant eigenvalue of authority (or hub) matrix
# iter = number of iterations
kleinberg.centrality = function(g, t = 3) {
A = as_adjacency_matrix(g, sparse=FALSE);
n = vcount(g);
# compute authority matrix
C = t(A) %*% A;
x0 = rep(0, n)
x1 = rep(1/n, n)
eps = 1/10^t
iter = 0
while (sum(abs(x0 - x1)) > eps) {
x0 = x1
x1 = x1 %*% C
m = x1[which.max(abs(x1))]
x1 = x1 / m
iter = iter + 1
}
y = x1 %*% t(A)
return(list(a = as.vector(x1), h = as.vector(y), val = m, iter = iter))
}
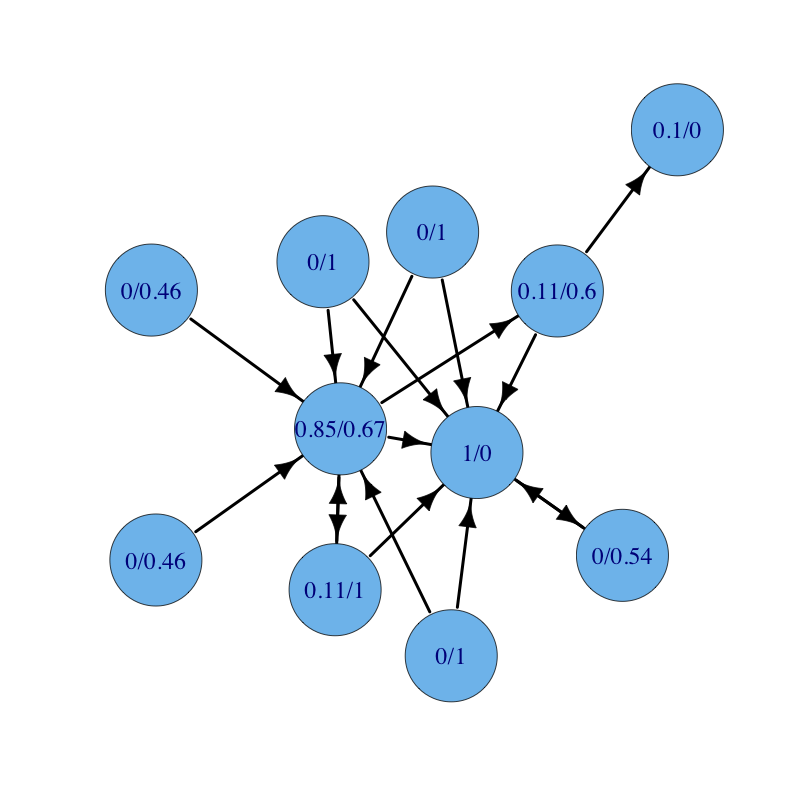
A directed graph with nodes labelled with their authority followed by their hub centralities. Notice that all types of nodes are present: authorities that are not hubs, hubs that are not authorities, authorities that are also hubs, and nodes that are neither authorities nor hubs. Mind also that there are nodes with null hub score but with positive out-degree, and nodes with null authority score with positive in-degree.

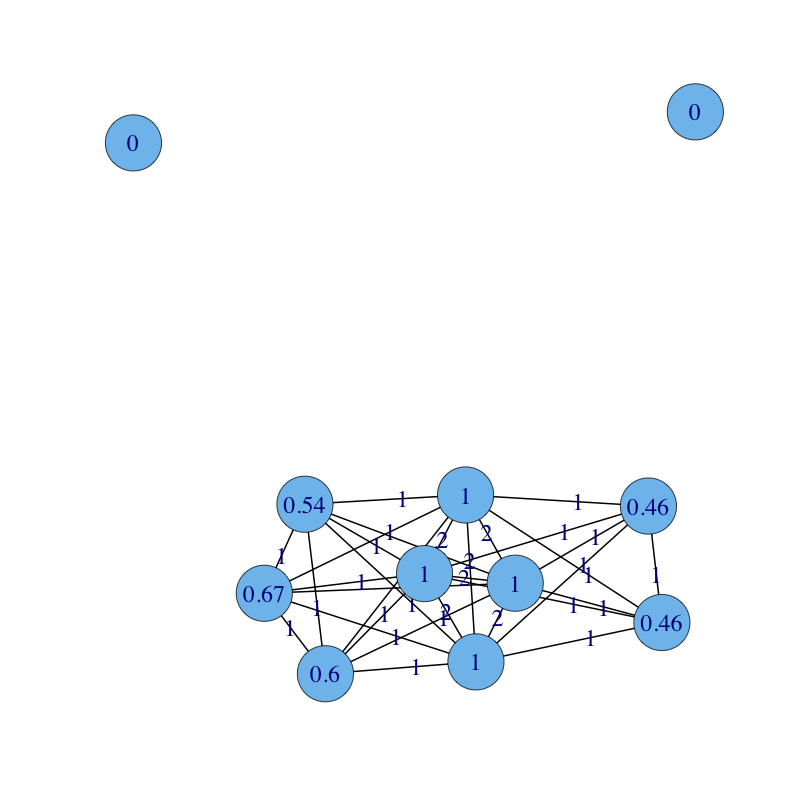
The undirected, weighted co-citation graph with nodes labelled with their authority scores. Authorities are central nodes in this graph with respect to weighted eigenvector centrality.
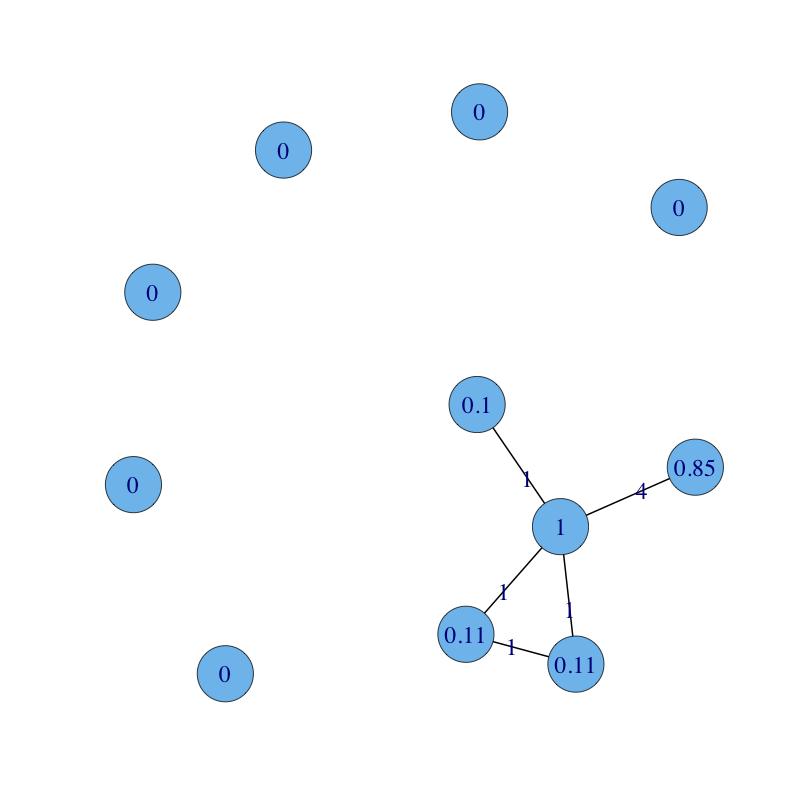
The undirected, weighted co-reference graph with nodes labelled with their hub scores. Hubs are central nodes in this graph with respect to weighted eigenvector centrality.