Degree Centrality

Degree is a simple centrality measure that counts how many neighbors a node has. If the network is directed, we have two versions of the measure: in-degree is the number of in-coming links, or the number of predecessor nodes; out-degree is the number of out-going links, or the number of successor nodes. Typically, we are interested in in-degree, since in-links are given by other nodes in the network, while out-links are determined by the node itself. Degree centrality thesis reads as follows:

A node is important if it has many neighbors, or, in the directed case, if there are many other nodes that link to it.

Math

Let $A = (a_{i,j})$ be the adjacency matrix of a directed graph. The in-degree centrality $x_{i}$ of node $i$ is given by: $$x_{i} = \sum_k a_{k,i}$$ or in matrix form ($e$ is a vector with all components equal to unity): $$x = e A$$ The out-degree centrality $y_{i}$ of node $i$ is given by: $$y_{i} = \sum_k a_{i,k}$$ or in matrix form: $$y = e A^T$$ Related to degree is friendship paradox, which is a phenomenon observed by sociologist Scott L. Feld. It claims that, on average,

I have fewer friends than my friends have :-(

On a social network, it formally says that the mean node degree: $$\mu_1 = \frac{\sum_i k_i}{n}$$ is less than or equal to the mean neighbors degree: $$\mu_2 = \frac{\sum_{i,j} a_{i,j} k_j}{\sum_{i,j} a_{i,j}}$$ Indeed: $$\mu_2 = \frac{\sum_{i,j} a_{i,j} k_j}{\sum_{i,j} a_{i,j}} = \frac{\sum_{j} \sum_{i} a_{i,j} k_j}{\sum_{j} \sum_{i} a_{i,j}} = \frac{\sum_j k_j \sum_i a_{i,j}}{\sum_j k_j} = \frac{\sum_j k_j \cdot k_j}{\sum_i k_i} = \frac{\langle k^2 \rangle}{\langle k \rangle}$$ where $\langle k^2 \rangle$ is the quadratic mean of degrees and $\langle k \rangle$ is the mean of degrees. Hence: $$\mu_2 - \mu_1 = \frac{\langle k^2 \rangle}{\langle k \rangle} - \langle k \rangle = \frac{\langle k^2 \rangle - \langle k \rangle^2}{\langle k \rangle} = \frac{\sigma^{2}}{\langle k \rangle} \geq 0$$ Since both the variance $\sigma^2$ and the mean $\langle k \rangle$ of the degree distribution are positive quantities, we have that the inequality holds. In particular we have that $\mu_1 = \mu_2$ if and only if $\sigma^2 = 0$ if and only if all nodes have the same degree (the graph is regular). On the other hand, when the distribution of degrees is skewed (the typical case), the inequality is proper. This because hub nodes, which are nodes with a high degree, are counted once in $\mu_1$, but are counted many times in $\mu_2$, because they are, by definition, friends on many others. Hence, the mean $\mu_2$ is computed on a biased sample.

Code

The built-in function degree computes degree centrality and strength computes weighted degree centrality.

A user-defined function degree.centrality follows:


# Degree centrality
# INPUT
# g = graph
# mode = degree mode ("in" for in-degree, "out" for out-degree, "all" for total degree)
degree.centrality = function(g, mode) {
  A = as_adjacency_matrix(g, sparse=FALSE);
  e = rep(1, n);
  if (mode == "in") x = e %*% A
  if (mode == "out") x = e %*% t(A) 
  if (mode == "all") x = e %*% (A + t(A)); 
  return(as.vector(x));
}

Example

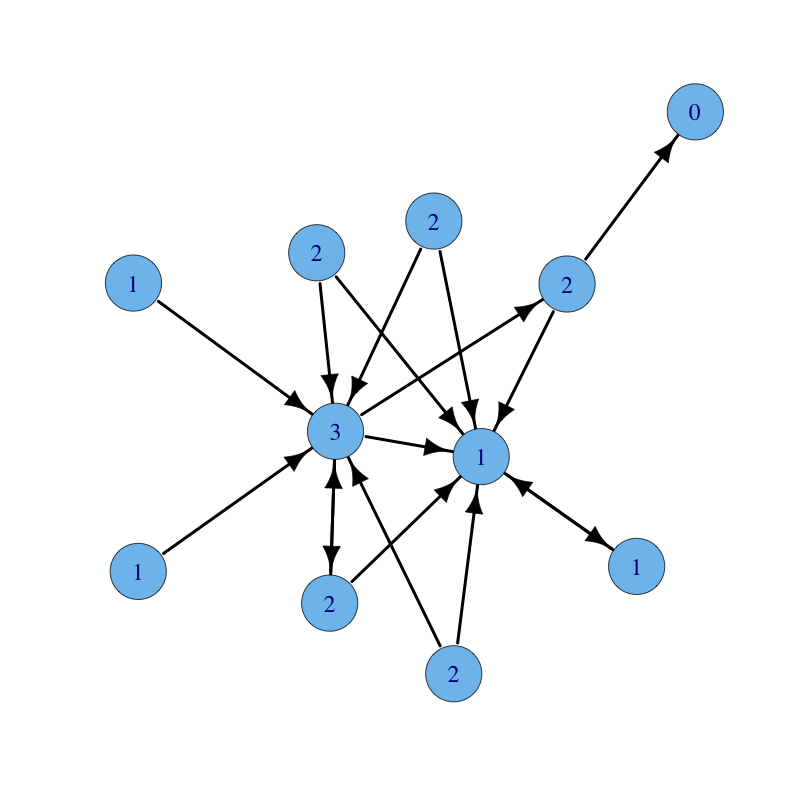
A graph with nodes labelled with their in-degree centrality follows:

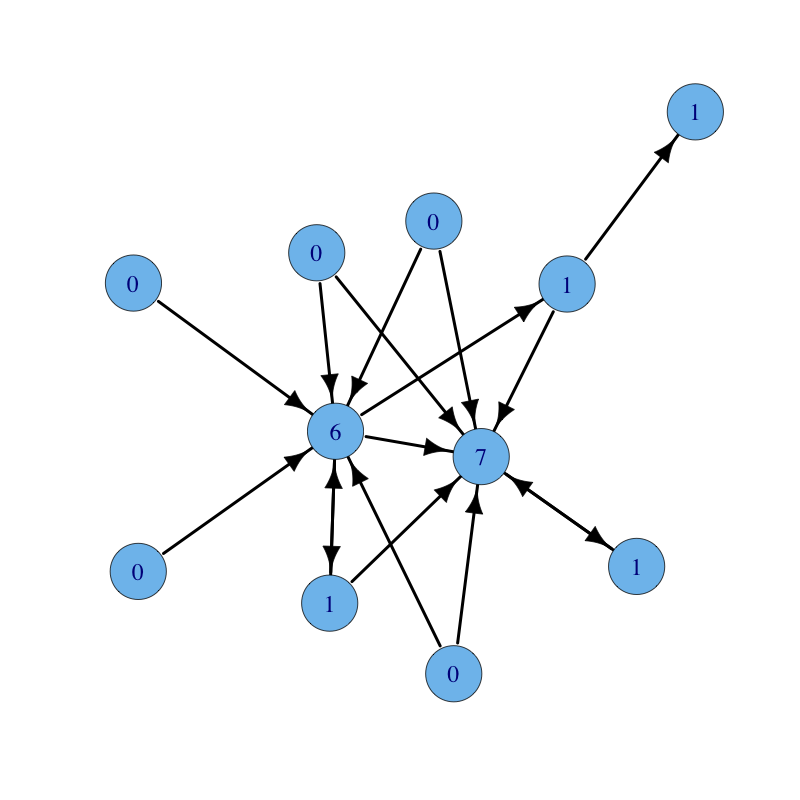
Next is the same graph with nodes labelled with their out-degree centrality: