Closeness Centrality

Closeness centrality measures the mean distance from a vertex to other vertices. Recall that a geodesic path is a shortest path through a network between two vertices. Suppose $d_{i,j}$ is the length of a geodesic path from $i$ to $j$, meaning the number of edges along the path. Then the mean geodesic distance for vertex $i$ is:

$\displaystyle{l_i = \frac{1}{n} \sum_j d_{i,j}}$

This quantity takes low values for vertices that are separated from others by only a short geodesic distance on average. Such vertices might have better access to information at other vertices or more direct influence on other vertices. In a social network, for instance, a person with lower mean distance to others might find that their opinions reach others in the community more quickly than the opinion of someone with higher mean distance. Some authors exclude from the sum the term $j = i$ for which $d_{i,i} = 0$ and hence divide the sum for $n-1$ instead of $n$.

The mean distance $l_i$ is not a centrality measure in the sense of the previous ones, since it gives low values to more central nodes and high values to less central ones, which is the opposite of other centrality measures. In the social network literature, therefore, researchers commonly calculate its inverse, called closeness centrality:

$\displaystyle{C_i = \frac{1}{l_i} = \frac{n}{\sum_j d_{i,j}}}$

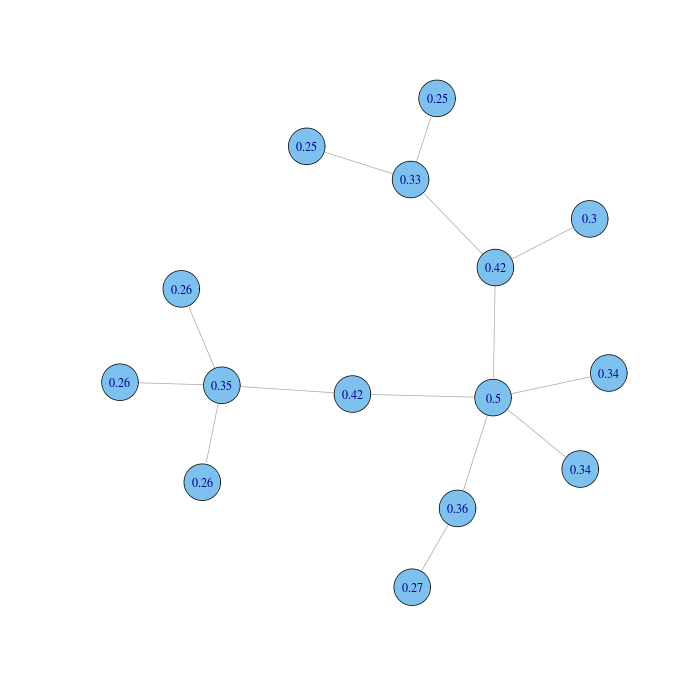
Function closeness (R) computes closeness centrality (this function uses $n-1$ as the numerator of the formula and assigns a distance equal to the number of nodes of the graph to pairs of nodes that are not reachable). This is a network with nodes labelled with their closeness centrality (the scores are rounded to the second decimal digit):

Closeness centrality differs from either degree or eigenvector centrality. For instance, consider a node A connected to a single other node B. Imagine that node B is very close to the other nodes in the graph, hence it has a large closeness score. It follows that node A has a relatively large closeness as well, since A can reach all the nodes that B reaches in only one additional step with respect to B. However, A has degree only 1, and its eigenvector score might not be impressive.

The largest possible value for the mean geodesic distance occurs for a root of a chain graph, a graph where the $n$ nodes form a linear sequence or chain, where the roots are the two ends of the chain. Using $n-1$ at the denominator of the mean, the mean distance from one root to the other vertices is

$\displaystyle{\frac{1}{n-1} \sum_{i=1}^{n-1} i = \frac{(n-1) n}{2 (n-1)} = \frac{n}{2}}$

There are some issue that deserve to be discussed about closeness centrality. One issue is that its values tend to span a rather small dynamic range from smallest to largest. Indeed, geodesic distances between vertices in most networks tend to be small, the typical and largest geodesic distances increasing only logarithmically with the size of the network. Hence the dynamic range of values of $l_i$ (and hence of $C_i$) is small.

This means that in practice it is difficult to distinguish between central and less central vertices using this measure. Moreover, even small fluctuations in the structure of the network can change the order of the values substantially. For instance, for the actor network, the network of who has appeared in films with who else, constructed from the Internet Movie Database, we find that in the largest component of the network, which includes 98% of all actors, the smallest mean distance $l_i$ of any actor is 2.4138 for the actor Christopher Lee (The Lord of the Rings), while the largest is 8.6681 for an Iranian actress named Leia Zanganeh. The ratio of the two is just 3.6 and about half a million actors lie in between. The second best centrality score belongs to Donald Pleasence, who scores 2.4164, very close to the winner. Other centrality measures typically don't suffer from this problem because they have a wider dynamic range and the centrality values, in particular those of the leaders, are widely separated.

A second issue about closeness centrality is that geodesic distance between two vertices is infinite if the vertices are not reachable through a path, hence $l_i$ is infinite and $C_i$ is zero for all vertices $i$ that do not reach all other vertices in the graph. The most common solution is to average the distance over only the reachable nodes. This gives us a finite measure, but distances tend to be smaller, hence closeness centrality scores tend to be larger, for nodes in small components. This is usually undesirable, since in most cases vertices in small components are considered less important than those in large components.

A second solution is to assign a distance equal to the number of nodes of the graph to pairs of vertices that are not connected by a path. This again will give a finite value for the closeness formula. Notice that the longest path in a graph with $n$ nodes has length $n-1$ edges, hence the assigned distance to unreachable nodes is one plus the maximum possible distance in the network.

A third solution is to compute closeness centrality only for those vertices in the largest connected component of the network. This is a good solution when the largest component is a giant one that covers the majority of the nodes.

A fourth (and last) solution is to redefine closeness centrality in terms of the harmonic mean distance between vertices, that is the average of the inverse distances:

$\displaystyle{C_i = \frac{1}{n-1} \sum_{j \neq i} \frac{1}{d_{i,j}}}$