In questa parte impareremo a disegnare una rete. Il codice che useremo è tratto dal libro Generative Design. Una rete è un insieme di punti, detti nodi, connessi da segmenti, detti archi. Useremo un algoritmo di visualizzazione basato su forze (force-directed). L'idea di questo algoritmo è la seguente:
La somma di queste due forze permette di ottenere una visualizzazione che disegna nodi connessi da archi vicini tra loro e nodi non connessi da archi più lontano. L'idea è che nodi connessi da un arco sono simili tra loro e gruppi di nodi simili vengono visualizzati nello stesso spazio.
La prima cosa da realizzare è la forza di attrazione tra due nodi. La repulsione è poi realizzata come una attrazione negativa. Consideriamo due nodi in movimento; uno di loro è un attrattore ed esercita una forza di attrazione sull'altro nodo modificandone il movimento. La forza di attrazione $f$ tra due nodi agisce entro un raggio di attrazione $r$ e dipende in modo inverso dalla distanza tra i nodi $d$: se $d$ è piccola (vicino a 0) allora la forza $f$ è grande, se invece $d$ è grande (vicino a $r$) allora la forza $f$ è piccola; infine la forza è nulla quando $d \geq r$. Possiamo modellare la forza di attrazione con questa formula: $$f = \frac{\sqrt{r} - \sqrt{d}}{\sqrt{d}} $$ assumendo che $f = 0$ se $d \geq r$. Notate che in questo modello la dipendenza è inversa rispetto alla radice quadrata della distanza; nella legge di gravitazione universale di Isaac Newton la forza dipende invece dall'inverso del quadrato della distanza.
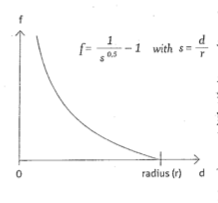
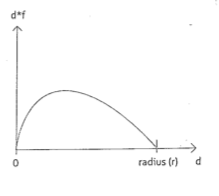
Possiamo applicare la forza di attrazione al nodo che viene attratto in questo modo. Ogni nodo è dotato di un vettore di movimento (che indica la velocità e la direzione del moto). La forza, calcolata come sopra, viene prima moltiplicata per il vettore distanza tra i due nodi coinvolti, ossia il vettore differenza tra i due nodi, ottenendo un vettore di attrazione. Si noti che: $$d \cdot f = \sqrt{d} (\sqrt{r} - \sqrt{d})$$ Il prodotto $d \cdot f$ è piccolo quando la distanza è piccola oppure quando la distanza è prossima al raggio di attrazione $r$, mentre è grande quando la distanza è in una posizione intermedia.
Possiamo quindi sommare il vettore di attrazione al vettore di movimento del nodo da attrarre modificandone la posizione.
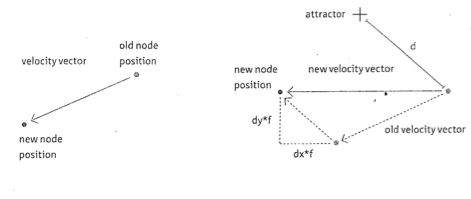
Infine una forza di repulsione si ottiene cambiando il segno al vettore di attrazione. Si veda la classe Node del codice scaricato.
La forza di attrazione tra due nodi connessi da un arco si realizza in questo modo. Immaginiamo un arco come una molla con una distanza a riposo pari a $l$. Se i due nodi distano più o meno di $l$, allora si muoveranno cercando di portarsi a tale distanza, avvicinandosi se la distanza è maggiore di $l$ o allontanandosi in caso contrario. L'applicazione della forza di attrazione tra i due nodi connessi è schematizzata nel seguente modo:
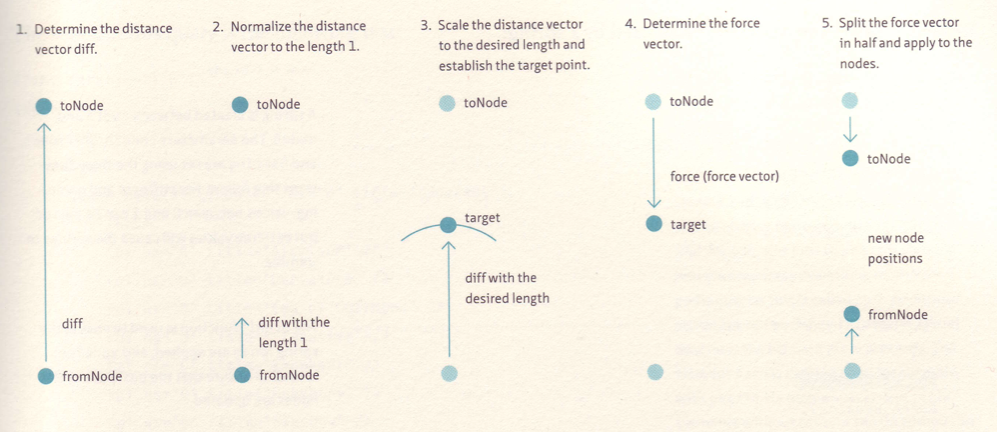
Si veda la classe Spring del codice scaricato.
Infine possiamo mettere assieme le due forze, la repulsione dei nodi e l'attrazione degli archi, per visualizzare la rete. Si veda lo sketch network del codice scaricato.